Adjacent and vertical angles and their properties. Adjacent and vertical angles

on topic: Related and vertical angles, their properties.

(3 lessons)

As a result of studying the topic you need:

BE ABLE TO:

Concepts: adjacent and vertical angles, perpendicular lines

Distinguish between adjacent and vertical angles

Adjacent and vertical angle theorems

Solve problems using the properties of adjacent and vertical angles

Properties of adjacent and vertical angles

Construct adjacent and vertical angles perpendicular to straight lines

LITERATURE:

1. Geometry. 7th grade. Zh. Kaydasov, G. Dosmagambetova, V. Abdiev. Almaty "Mektep". 2012

2. Geometry. 7th grade. K.O.Bukubaeva, A.T. Mirazova. Almaty "Atamura" 2012

3. Geometry. 7th grade. Methodical manual. K.O. Bukubaeva. Almaty "Atamura" 2012

4. Geometry. 7th grade. Didactic material. A.N. Shynybekov. Almaty "Atamura" 2012

5. Geometry. 7th grade. Collection of tasks and exercises. K.O. Bukubaeva, A.T. Mirazova. Almaty "Atamura" 2012

Remember that you need to work according to the algorithm!

Don't forget to check, make notes in the margins,

Please do not leave any questions you have unanswered.

Be objective during mutual verification, it will help both you and the person

who are you checking?

I WISH YOU SUCCESS!

TASK No. 1.

Read the definition and learn (2b):

Definition. Angles in which one side is common and the other two sides are additional rays are called adjacent.

2) Learn and write the theorem in your notebook: (2b)

Sum adjacent corners equals 180.

Given:

∠ ANM and∠ DOV – data adjacent angles

OD - common side

Prove:

∠ AOD +∠ DOV = 180

Proof:

Based on the axiomIII 4:

∠ AOD +∠ DOV =∠ AOB.

∠ AOB - expanded. Hence,

∠ AOD +∠ DOV = 180

The theorem has been proven.

3) From the theorem it follows: (2b)

1) If two angles are equal, then their adjacent angles are equal;

2) if adjacent angles are equal, then the degree measure of each of them is 90°.

Remember!

An angle equal to 90° is called a right angle.

An angle less than 90° is called an acute angle.

An angle greater than 90° and less than 180° is called an obtuse angle.

Right angle Acute angle Obtuse angle

Since the sum of adjacent angles is 180°, then

1) an angle adjacent to a right angle, straight;

2) the angle adjacent to the acute angle is obtuse;

3) an angle adjacent to an obtuse angle is acute.

4) Consider a sample solutionadachi:

a) Given:∠ hkAnd∠ kl- adjacent;∠ hkmore∠ klat 50°.

Find:∠ hkAnd∠ kl.

Solution: Let∠ kl= x, then∠ hk= x + 50°. By the property of the sum of adjacent angles∠ kl + ∠ hk= 180°.

x + x + 50° = 180°;

2x = 180° - 50°;

2x = 130°;

x = 65°.

∠ kl= 65°;∠ hk= 65°+ 50° = 115°.

Answer: 115° and 65°.

b) Let∠ kl= x, then∠ hk= 3x

x + 3x = 180°; 4x = 180°; x = 45°;∠ kl= 45°;∠ hk= 135°.

Answer: 135° and 45°.

5) Working with determining adjacent angles: (2 b)

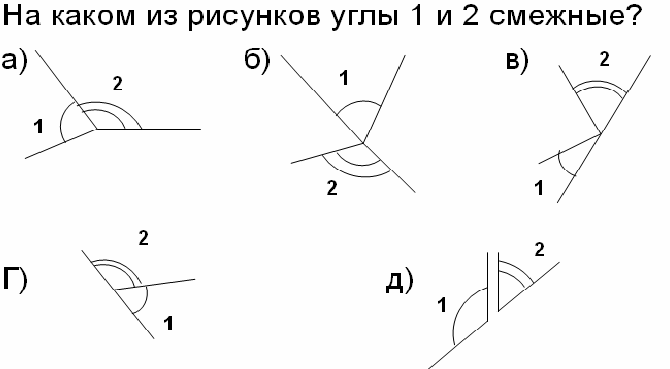
6) Find errors in definitions: (2b)

Pass test #1

Task No. 2

1) Construct 2 adjacent angles so that their common side passes through point C and the side of one of the angles coincides with ray AB. (2b)

2). Practical work to discover the properties of adjacent angles: (5b)

Work progress

1. Construct an angleadjacent cornerA , IfA : sharp, straight, blunt.

2. Measure the angles.

3. Enter the measurement data into the table.

4. Find the relationship between the anglesA And.

5. Draw a conclusion about the property of adjacent angles.

Pass test #2

Task No. 3

Draw the unexpanded∠ AOB and name the rays that are the sides of this angle.

Draw ray O, which is a continuation of ray OA, and ray OD, which is a continuation of ray OB.

Write in your notebook: angles∠ AOB and∠ SODs are called vertical. (3b)

Learn and write in your notebook: (4b)

Definition: Angles in which the sides of one of them are complementary rays of the other are calledvertical corners.

< 1 and<2, <3 и <4 vertical angles

RaysOFAndO.A. , O.C.AndO.E.are pairwise complementary rays.

Theorem: Vertical angles are equal.

Proof.

Vertical angles are formed when two straight lines intersect. Let straight lines a andbintersect at point O.∠ 1 and∠ 2 – vertical angles.

∠ AOC-expanded, meaning∠ AOC = 180°. However∠ 1+ ∠ 2= ∠ AOC, i.e.

∠ 3+ ∠ 1= 180°, from here we have:

∠ 1= 180 - ∠ 3. (1)

We also have that∠ DOV = 180°, from here∠ 2+ ∠ 3= 180°, or∠ 2= 180°- ∠ 3. (2)

Since in equalities (1) and (2) the straight parts are equal, then∠ 1= ∠ 2.

The theorem has been proven.

5). Working with determining vertical angles: (2b)

6) Find the error in the definition: (2b).

Pass test #3

Task No. 4

1) Practical work on discovering the properties of vertical angles: (5b)

Work progress:

1. Construct the angle β vertical angleα , Ifα :

sharp, straight, blunt.

2.Measure the angles.

3. Enter the measurement data into the table

4. Find the relationship between the angles α and β.

5.Draw a conclusion about the properties of vertical angles.

2) Proof of the properties of adjacent and vertical angles. (3b)

2) Consider a sample solutionadachi.

Task. Lines AB and CD intersect at point O so that∠ AOD = 35°. Find the angles AOC and BOC.

Solution:

1) Angles AOD and AOS are adjacent, therefore∠ BOC= 180° - 35° = 145°.

2) Angles AOC and BOC are also adjacent, therefore∠ BOC= 180° - 145° = 35°.

Means,∠ BOC = ∠ AOD = 35°, and these angles are vertical. Question: Is it true that all vertical angles are equal?

3) Solving problems on finished drawings: (3b)

1. Find the angles AOB, AOD, COD.

3) Find angles BOC, FOA.: (3b)

3. Find adjacent and vertical angles in the figure. Let the values of the two angles marked in the drawing be known, 28? and 90?. Is it possible to find the values of the remaining angles without performing measurements (2b)

Pass test number 4

Task No. 5

Test your knowledge by completingtest work No. 1

Task No. 6

1) Prove the properties of vertical angles yourself and write these proofs in your notebook. (3b)

Students independently, using the properties of vertical and adjacent angles, must justify the fact that if, when two straight lines intersect, one of the resulting angles is a straight line, then the remaining angles are also right angles.

2) Solve two problems to choose from:

1.The degree measures of adjacent angles are in the ratio 7:2. Find these angles. (2b)

2. One of the angles formed when two straight lines intersect is 11 times smaller than the other. Find each of the angles. (3b)

3. Find adjacent angles if their difference and their sum are in the ratio 2:9. (3b)

Task No. 7

Well done! You can begin test work No. 2.

Test work No. 1.

Decide to choose any of the options (10b)

Option 1

<1 и <2,

<3 и <2,

G)<1 и <3. Какие это углы?

e) Draw (by eye) an angle of 30° and< ABC, adjacent to the given one

f) What angles are called vertical?

Two angles are called vertical if they are equal.

g) From point A draw two lines perpendicular to the lineA

You can only draw one straight line.

Option 2

1. The student, answering the teacher’s questions, gave appropriate answers. Check if they are correct by marking the words “YES”, “NO”, “DON’T KNOW” in the third column. If “NO”, write down the correct answer there or add the missing one.

<1 и <4,

<2 и <4

D)<1 и < 3 смежные?

No. They are vertical

E) Which lines are called perpendicular?

Two lines are called perpendicular if they intersect at right angles

G) Draw vertical angles so that their sides are perpendicular to straight lines.

2. Name the vertical angles in this figure.

Total: 10 points

“5” -10 points;

“4” -8-9 points;

"3" -5-7 points.

Test work No. 2.

Decide to choose any option

Option I

Find adjacent angles if their difference and their sum are in the ratio 2:9. (4b)

Find all the angles formed by the intersection of two straight lines if one of them is 240° less than the sum of the other two. (6b)

Option II

1) Find adjacent angles if their difference and their sum are in the ratio 5:8(4b)

2) Find all the undeveloped angles formed at the intersection of two straight lines, if one of them is 60° greater than the sum of the other two. (6b)

Total: 10 points

“5” -10 points;

“4” -8-9 points;

"3" -5-7 points.

CHAPTER I.

BASIC CONCEPTS.

§11. ADJACENT AND VERTICAL CORNERS.

1. Adjacent angles.

If we extend the side of any angle beyond its vertex, we get two angles (Fig. 72): / And the sun and / SVD, in which one side BC is common, and the other two A and BD form a straight line.

Two angles in which one side is common and the other two form a straight line are called adjacent angles.

Adjacent angles can also be obtained in this way: if we draw a ray from some point on a line (not lying on a given line), we will obtain adjacent angles.
For example, / ADF and / FDВ - adjacent angles (Fig. 73).

Adjacent angles can have a wide variety of positions (Fig. 74).

Adjacent angles add up to a straight angle, so the umma of two adjacent angles is equal 2d.

Hence, a right angle can be defined as an angle equal to its adjacent angle.

Knowing the size of one of the adjacent angles, we can find the size of the other angle adjacent to it.

For example, if one of the adjacent angles is 3/5 d, then the second angle will be equal to:

2d- 3 / 5 d= l 2 / 5 d.

2. Vertical angles.

If we extend the sides of the angle beyond its vertex, we get vertical angles. In drawing 75, the angles EOF and AOC are vertical; angles AOE and COF are also vertical.

Two angles are called vertical if the sides of one angle are continuations of the sides of the other angle.

Let / 1 = 7 / 8 d(Figure 76). Adjacent to it / 2 will be equal to 2 d- 7 / 8 d, i.e. 1 1/8 d.

In the same way you can calculate what they are equal to / 3 and / 4.
/ 3 = 2d - 1 1 / 8 d = 7 / 8 d; / 4 = 2d - 7 / 8 d = 1 1 / 8 d(Diagram 77).

We see that / 1 = / 3 and / 2 = / 4.

You can solve several more of the same problems, and each time you will get the same result: the vertical angles are equal to each other.

However, to make sure that vertical angles are always equal to each other, it is not enough to consider individual numerical examples, since conclusions drawn from particular examples can sometimes be erroneous.

It is necessary to verify the validity of the properties of vertical angles by reasoning, by proof.

The proof can be carried out as follows (Fig. 78):

/ a+/ c = 2d;
/ b+/ c = 2d;

(since the sum of adjacent angles is 2 d).

/ a+/ c = / b+/ c

(since the left side of this equality is also equal to 2 d, and its right side is also equal to 2 d).

This equality includes the same angle With.

If we subtract equal amounts from equal quantities, then equal amounts will remain. The result will be: / a = / b, i.e. the vertical angles are equal to each other.

When considering the issue of vertical angles, we first explained which angles are called vertical, i.e. definition vertical angles.

Then we made a judgment (statement) about the equality of the vertical angles and were convinced of the validity of this judgment through proof. Such judgments, the validity of which must be proven, are called theorems. Thus, in this section we gave a definition of vertical angles, and also stated and proved a theorem about their properties.

In the future, when studying geometry, we will constantly have to encounter definitions and proofs of theorems.

3. The sum of angles that have a common vertex.

On the drawing 79 / 1, / 2, / 3 and / 4 are located on one side of a line and have a common vertex on this line. In sum, these angles make up a straight angle, i.e.
/ 1+ / 2+/ 3+ / 4 = 2d.

On the drawing 80 / 1, / 2, / 3, / 4 and / 5 have a common vertex. In sum, these angles make up a full angle, i.e. / 1 + / 2 + / 3 + / 4 + / 5 = 4d.

Exercises.

1. One of the adjacent angles is 0.72 d. Calculate the angle formed by the bisectors of these adjacent angles.

2. Prove that the bisectors of two adjacent angles form a right angle.

3. Prove that if two angles are equal, then their adjacent angles are also equal.

4. How many pairs of adjacent angles are there in the drawing 81?

5. Can a pair of adjacent angles consist of two acute angles? from two obtuse angles? from right and obtuse angles? from a right and acute angle?

6. If one of the adjacent angles is right, then what can be said about the size of the angle adjacent to it?

7. If at the intersection of two straight lines one angle is right, then what can be said about the size of the other three angles?

In this lesson we will look at and understand the concept of adjacent angles. Let's consider a theorem that concerns them. Let us introduce the concept of “vertical angles”. Let's look at some supporting facts about these angles. Next, we formulate and prove two corollaries about the angle between the bisectors of vertical angles. At the end of the lesson we will look at several problems on this topic.

Let's start our lesson with the concept of “adjacent angles”. Figure 1 shows the developed angle ∠AOC and the ray OB, which divides this angle into 2 angles.

Rice. 1. Angle ∠AOC

Let's consider the angles ∠AOB and ∠BOC. It is quite obvious that they have a common side VO, and the sides AO and OS are opposite. Rays OA and OS complement each other, which means they lie on the same straight line. Angles ∠AOB and ∠BOC are adjacent.

Definition: If two angles have a common side, and the other two sides are complementary rays, then these angles are called adjacent.

Theorem 1: The sum of adjacent angles is 180 o.

Rice. 2. Drawing for Theorem 1

∠MOL + ∠LON = 180 o. This statement is true, since the ray OL divides the unfolded angle ∠MON into two adjacent angles. That is, we do not know the degree measures of any of the adjacent angles, but we only know their sum - 180 degrees.

Consider the intersection of two lines. The figure shows the intersection of two lines at point O.

Rice. 3. Vertical angles ∠ВОА and ∠СOD

Definition: If the sides of one angle are a continuation of the second angle, then such angles are called vertical. That is why the figure shows two pairs of vertical angles: ∠AOB and ∠COD, as well as ∠AOD and ∠BOC.

Theorem 2: Vertical angles are equal.

Let's use Figure 3. Consider the rotated angle ∠AOC. ∠AOB = ∠AOC - ∠BOC = 180 o - β. Let's consider the developed angle ∠BOD. ∠COD = ∠BОD - ∠BOC = 180 o - β.

From these considerations we conclude that ∠AOB = ∠COD = α. Similarly, ∠AOD = ∠BOS = β.

Corollary 1: The angle between the bisectors of adjacent angles is 90°.

Rice. 4. Drawing for Corollary 1

Since OL is the bisector of the angle ∠BOA, then the angle ∠LOB = , similarly to ∠BOA = . ∠LOK = ∠LOB + ∠BOK = + = . The sum of angles α + β is equal to 180°, since these angles are adjacent.

Corollary 2: The angle between the bisectors of vertical angles is 180°.

Rice. 5. Drawing for Corollary 2

KO is the bisector ∠AOB, LO is the bisector ∠COD. Obviously, ∠KOL = ∠KOB + ∠BOC + ∠COL = o. The sum of angles α + β is equal to 180°, since these angles are adjacent.

Let's consider some tasks:

Find the angle adjacent to ∠AOC if ∠AOC = 111 o.

Let's make a drawing for the task:

Rice. 6. Drawing for example 1

Since ∠AOC = β and ∠COD = α are adjacent angles, then α + β = 180 o. That is, 111 o + β = 180 o.

This means β = 69 o.

This type of problem exploits the sum of adjacent angles theorem.

One of the adjacent angles is a right angle, what is the other angle (acute, obtuse or right)?

If one of the angles is right, and the sum of the two angles is 180°, then the other angle is also right. This problem tests knowledge about the sum of adjacent angles.

Is it true that if adjacent angles are equal, then they are right angles?

Let's make an equation: α + β = 180 o, but since α = β, then β + β = 180 o, which means β = 90 o.

Answer: Yes, the statement is true.

Two equal angles are given. Is it true that the angles adjacent to them will also be equal?

Rice. 7. Drawing for example 4

If two angles are equal to α, then their corresponding adjacent angles will be 180 o - α. That is, they will be equal to each other.

Answer: The statement is correct.

Alexandrov A.D., Werner A.L., Ryzhik V.I. and others. Geometry 7. - M.: Education.
Atanasyan L.S., Butuzov V.F., Kadomtsev S.B. and others. Geometry 7. 5th ed. - M.: Enlightenment.
\Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometry 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, edited by V.A. Sadovnichigo. - M.: Education, 2010.

Measurement of segments ().
General lesson on geometry in 7th grade ().
Straight line, segment ().

No. 13, 14. Butuzov V.F., Kadomtsev S.B., Prasolova V.V. Geometry 7 / V.F. Butuzova, S.B. Kadomtsev, V.V. Prasolov, edited by V.A. Sadovnichigo. - M.: Education, 2010.
Find two adjacent angles if one is 4 times the other.
Given the angle. Construct adjacent and vertical angles for it. How many such angles can be constructed?
* In which case are more pairs of vertical angles obtained: when three straight lines intersect at one point or at three points?

Equal to two right angles .

Given two adjacent angles: AOB And VOS. It is required to prove that:

∠AOB+∠BOS=d+ d = 2d

Let's restore from the point ABOUT to a straight line AC perpendicular O.D.. We divided the angle AOB into two parts AOD and DOB so that we can write:

∠AOB = ∠ A.O.D+∠ DO.B.

Let us add to both sides of this equality the same angle BOC, why equality will not be violated:

∠ A.O.B + ∠ B.O.WITH= ∠AOD + ∠ DO.B. + ∠ B.O.WITH

Since the amount DO.B. + BOC amounts to right angle DOWITH, That

∠ A.O.B+ ∠ B.O.WITH= ∠ A.O.D + ∠ DOWITH= d + d = 2 d,

Q.E.D.

Consequences.

1. Sum of angles (A.O.B,BOC, СOD, DOE), located around a common vertex (O) on one side of the straight line ( A.E.) is equal to 2 d= 180 0 , because this amount is the sum of two adjacent corners, for example these: AOC + COE

2. Sum of angles located around a common peaks (O) on both sides of any straight line is equal to 4 d=360 0,

Converse theorem.

If sum of two angles, having a common vertex and a common side and not covering each other, is equal to two right angles (2d), then such angles are adjacent, i.e. their other two sides are straight line.

If from one point (O) of a straight line (AB) we restore perpendiculars to it, on each side, then these perpendiculars form one straight line (CD). From any point outside a line you can drop to this line perpendicular and only one at that.

Because sum of angles COB And BOD equals 2d.

StraightWITH parts of which OWITH And O.D. serve as perpendiculars to a line AB, is called a line perpendicular to AB.

If straight WITHD perpendicular to the line AB, then vice versa: AB perpendicular to WITHD, because parts O.A. And O.B. also serve perpendicular to WITHD. Therefore straight AB And WITHD are called mutually perpendicular.

That two are straight AB And WITHD mutually perpendicular, expressed in writing as follows AB^ WITHD.

The two angles are called vertical, if the sides of one are a continuation of the sides of the other.

So, at the intersection of two lines AB And WITHD two pairs of vertical angles are formed: A.O.D And COB; AOC And DO.B. .

Theorem.

Two vertical angle equal .

Let two vertical angles be given: AOD And WITHO.B. those. O.B. there is a sequel O.A., A OWITH continuation O.D..

It is required to prove that AOD = WITHO.B.

Based on the property of adjacent angles, we can write:

A.O.D + DO.B.= 2 d

DOB + BOC = 2d

Means: AOD + DOB = DOB + BOC.

If we subtract from both sides of this equality by angle DO.B., we get:

A.O.D = BOC, which was what needed to be proven.

We will similarly prove that AOC = DO.B..

Adjacent angles- two angles in which one side is common, and the other two are continuations of one another.

The sum of adjacent angles is 180°

Vertical angles- these are two angles in which the sides of one angle are continuations of the sides of the other.

Vertical angles are equal.

2. Signs of equality of triangles:

I sign: If two sides and the angle between them of one triangle are respectively equal to two sides and the angle between them of another triangle, then such triangles are congruent.

II sign: If the sides and two adjacent angles of one triangle are respectively equal to the side and two adjacent angles of another triangle, then such triangles are congruent.

III sign: If three sides of one triangle are respectively equal to three sides of another triangle, then such triangles are congruent

3. Signs of parallelism of two straight lines: one-sided angles, lying crosswise and corresponding:

Two lines in a plane are called parallel, if they do not intersect.

Crosswise angles: 3 and 5, 4 and 6;

One-sided angles: 4 and 5, 3 and 6; rice. Page 55

Corresponding angles: 1 and 5, 4 and 8, 2 and 6, 3 and 7;

Theorem: If, when two lines intersect with a transversal, the lying angles are equal, then the lines are parallel.

Theorem: If, when two lines intersect with a transversal, the corresponding angles are equal, then the lines are parallel.

Theorem: If, when two lines intersect with a transversal, the sum of the one-sided angles is 180°, then the lines are parallel.

Theorem: if two parallel lines are intersected by a transversal, then the intersecting angles are equal

Theorem: if two parallel lines are intersected by a transversal, then the corresponding angles are equal

Theorem: if two parallel lines are intersected by a transversal, then the sum of one-sided angles is 180°

4. Sum of triangle angles:

The sum of the angles of a triangle is 180°

5. Properties of an isosceles triangle:

Theorem: In an isosceles triangle, the base angles are equal.

Theorem: In an isosceles triangle, the bisector drawn to the base is the median and the altitude (the median is the opposite), (the bisector bisects the angle, the median bisects the side, the altitude forms an angle of 90°)

Sign: If two angles of a triangle are equal, then the triangle is isosceles.

6. Right Triangle:

Right triangle- is a triangle in which one angle is right (that is, 90 degrees)

In a right triangle, the hypotenuse is longer than the leg

1. The sum of two acute angles of a right triangle is 90°

2. A leg of a right triangle lying opposite an angle of 30° is equal to half the hypotenuse

3. If a leg of a right triangle is equal to half the hypotenuse, then the angle opposite this leg is 30°

7. Equilateral triangle:

EQUILATERAL TRIANGLE, a flat figure having three sides of equal length; the three internal angles formed by the sides are also equal and amount to 60 °C.

8. Sin, cos, tg, ctg:

Sin= , Cos= , tg= , ctg= , tg= ,ctg=

9. Signs of a quadrilateral^

The sum of the angles of a quadrilateral is 2 π = 360°.

A quadrilateral can be inscribed in a circle if and only if the sum of the opposite angles is 180°

10. Signs of similarity of triangles:

I sign: if two angles of one triangle are respectively equal to two angles of another, then such triangles are similar

II sign: If two sides of one triangle are proportional to two sides of another triangle and the angles between these sides are equal, then such triangles are similar.

III sign: if three sides of one triangle are proportional to three sides of another, then such triangles are similar

11. Formulas:

· Pythagorean theorem: a 2 +b 2 =c 2

· sin theorem: