§5 Решение систем n уравнений из n неизвестными. Калькулятор онлайн

Метод Гаусса решения систем линейных алгебраических уравнений состоит в последовательном исключении неизвестных с помощью элементарных преобразований и сведении к верхней треугольной (ступенчатой или трапециевидной). После чего решают систему с конца к началу, подстановкой найденных решений.

Рассмотрим примеры решения систем линейных уравнений методом Гаусса, взяв за справочник сборник задач Дубовика В.П., Юрика И.И. "Высшая математика".

-------------

Решить систему линейных алгебраических уравнений.

1) Преобразуем исходную систему к ступенчатому виду. Для этого от второго уравнения вычтем первое, умноженное на 3, а от четвертого вычтем первое, умноженное на 4.

В результате с третьего уравнения имеем Полученное значение подставляем в исходное уравнение для нахождения

Полученные значения подставляем в первое уравнение

Решением системы трех линейных уравнений будут следующие значения переменных

2) Имеем систему трех уравнений с четырьмя неизвестными. В таких случаях одна переменная может быть свободна, а остальные будут выражаться через нее. Сведем систему к ступенчатому виду. Для этого от второго и третьего уравнения вычтем первое

Из последних двух уравнений получаем идентичные решения

После подстановки в первое уравнение получим

Данное уравнение связывает три переменные. Таким образом любая из переменных может быть выражена через две других

Итак получим следующее решение

3) Имеем разреженную систему линейных уравнений пятого порядка с пятью неизвестными. Сведем ее к ступенчатому виду. От второго уравнения вычтем первое и запишем в удобном для анализа виде

Из второго уравнения находим, что . Подставляем значения во все нижние уравнения и переносим за знак равенства. Также поменяем второе с третьим уравнения местами

Четвёртое и пятое уравнения эквивалентны. Выразим одну из переменных через другую

Полученное значение подставим во второе уравнение и найдем

Из первого уравнения определяем

Решение системы уравнений следующее

При вычислениях систем линейных алгебраических уравнений методом Гаусса нужно свезти систему линейных уравнений к ступенчатому виду. Для этого удобно записывать переменные под переменными, как в последнем примере, это ускорит решение. Остальное все зависит от матрицы, которую нужно решить и Ваших умений.

5.1. Правило Крамера

Установив основные свойства и способы вычисления определителей матриц любого порядка, возвратимся к основной задаче - решению и исследованию систем уравнений 1-ого порядка. Начнем изучение этого вопроса с разбора того основного случая, когда число уравнений совпадает с числом неизвестных.

Помножим все члены 1-го уравнения системы (1) на А 11 - алгебраическое дополнение элемента а 11 матрицы А, все члены 2-го уравнения системы (1) на А 21 - алгебраическое дополнение элемента а 21 матрицы А, наконец, все члены n-го уравнения системы (1) на А n1 - алгебраическое дополнение элемента а n1 матрицы А. Тогда получим систему

(1")

Прибавим почленно все уравнения системы, получим

(a i1 A i1)x 1 +(a i2 A i1)x 2 +...+(a in A i1)x n =b i A i1

Согласно теоремы про алгебраические дополнения имеем

a i1 A i1 =det A a i2 A i1 =0, ........., a in A i1 =0

Поэтому полученное уравнение можно переписать в виде

Рассмотрим матрицу

Полученную из матрицы А заменой элементов 1-го столбца столбцом свободных членов уравнений системы. Раскладывая det B1 по элементам 1-го столбца, получим det B 1 =b i A i1 , а потому

Аналогично, умножив уравнения системы (1) соответственно на Аі2 (и=1, 2, ... n) и добавляя их, получим

Поступив таким образом и в дальнейшем, получим систему уравнений

(2),

Где матрица Вk получена из А заменой k-го столбца столбцом свободных членов. Очевидно, любое решение системы (1) является и решением системы (2).

(3)

Напомним, что формулы (3) получены с предположением, что система (1) имеет решение. Непосредственной подстановкой найденных значений Х і в систему (1) можно убедиться в том, что они являются решением системы (1) и, следовательно, в предположении, что
, система (1) имеет решение и к тому же единственное.

^ Теорема (теорема Крамера): если определитель основной матрицы системы п уравнений 1-го порядка с п неизвестными отличный от нуля, тогда система имеет единственное решение. При этом значение каждого из неизвестных равно части от деления определителей двух матриц: в знаменателе стоит определитель основной матрицы системы, а в числителе определитель матрицы, полученной из основной матрицы системы заменой столбца, что отвечает выбранному неизвестному, столбцом свободных членов.

Из этой теоремы выходит, что если система уравнений однородная то есть свободные члены во всех уравнениях системы равны нулю, и если определитель основной матрицы системы отличный от нуля, тогда система имеет только нулевое решение. Действительно, в таком случае, матрицы, определители которых стоят в числителе формул (3), содержат столбец, который включает в себя лишь нули, и, следовательно, все числа Х і равны нулю. Из доказанного вытекает следующая теорема:

^ Если система п однородных уравнений 1-го порядка с п неизвестными имеет хотя бы одно ненулевое решение, тогда определитель основной матрицы системы равен нулю. Действительно, если бы этот определитель был не равен нулю, тогда система имела бы только нулевое решение, что противоречит условию.

В дальнейшем мы докажем, что равенство нулю определителя системы есть не только обязательное, необходимое условие существования ненулевого решения, но и условие, достаточное для существования такого решения. Иначе говоря, если определитель системы однородных уравнений равен нулю, тогда система имеет ненулевое решение (и при этом бесконечное множество таких решений).

^ 5.2. Решение и исследование систем уравнений первого порядка методом полного исключения (Метод Гаусса).

Формулы Крамера дают возможность, используя прием вычисления определителей, найти числовые значения решения системы уравнений в случае, когда определитель основной матрицы системы отличный от нуля. Но практическое применение этих формул во многих случаях усложнено. Прежде всего, необходимо отметить, что для нахождения решений по формулам (3) необходимо вычислить n+1 определитель n-го порядка, что представляет собой довольно трудоемкую работу, даже при использовании тех приемов, которые были указаны в §4. Но самое главное то, что в случае, когда коэффициенты уравнения заданы приближенно (в реальных задачах это бывает почти всегда), погрешность решения может быть довольно большая. Это объясняется тем, что слагаемые, которые входят в каждый из определителей, через которые определяется решение системы, могут быть довольно большие (напомним, они представляют собою произведение n сомножителей - различных коэффициентов расширенной матрицы системы), а сам определитель, который представляет собой алгебраическую сумму таких слагаемых, может быть малый. Даже в том случае, когда коэффициенты в системе исходных уравнений известны точно, но сами вычисления ведутся с учетом лишь заданного числа значащих цифр, мы по тем же причинам сможем получить довольно большие погрешности в результате. А потому при практическом решении систем уравнений в большинстве случаев используют не формулы Крамера, а другие приемы вычислений.

В данном курсе мы рассмотрим метод полного исключения, относительно решения систем уравнений 1-ого порядка также и в том случае, когда число уравнений не совпадает с числом неизвестных. Но изложение этого метода начнем с основного случая: когда число уравнений совпадает с числом неизвестных.

Таким образом, пусть снова задана система n уравнений с n неизвестными:

(1)

Поскольку хотя бы один из коэффициентов a i1 отличный от нуля (иначе в систему вообще не входило бы х1), и уравнения в системе возможно менять местами, тогда без какого-либо ограничения всеобщности можно считать, что
Поделим 1-е уравнение системы на a11 и приведем его к виду ,

Перемножая все члены полученного уравнения на аі1 и вычитая из і -го уравнения системы (1), получим новую систему

(2),

i=1, 2, ..., n; k=1, 2, ... , n

Поскольку уравнения системы (2) получены как линейные комбинации уравнений системы (1), то любое решение системы (1) является также и решением системы (2). Вместе с тем поскольку

То уравнения системы (1) могут быть получены как линейная комбинация уравнений системы (2). Следовательно, любое решение системы (2) является и решением системы (1). Таким образом, система (1) и (2) равнозначны. (Линейной комбинацией двух уравнений с 11 х 1 +с 12 х 2 +...+с 1n х n =d 1 і, с 21 х 1 +с 22 х 2 +...+с 2n х n =d 2 будем называть уравнение  1 (c 11 x 1 +c 12 x 2 +...+c 1n x n) + 2 (c 21 x 1 +c 22 x 2 +...+c 2n x n)= 1 d 1 + 2 d 2 , где  1 та  2 - числа)

Сравним теперь определители D1 и D2 основных матриц систем (1) и (2). Первая строка основной матрицы системы (2) получена из первой строки основной матрицы системы (1) делением на а 11 . Такая операция отвечает делению D1 на а11. Другие строки получены вычитанием из соответствующих строк основной матрицы системы (1) величин, пропорциональных первой строке. Эта операция не изменяет величины определителя. Отсюда выходит, что определитель D2 основной матрицы системы (2) равен . А потому
, если
и D2=0, если D1=0. Отметим, наконец, что вычисления мы проводили только с коэффициентами уравнений системы (1), поэтому нет необходимости писать сами уравнения. Достаточно написать лишь расширенную матрицу системы и преобразовать только элементы этой матрицы.

Будем обозначать переход от одной расширенной матрицы к другой, то есть фактически переход от одной системы уравнений к системе, ей равнозначной, символом или
. Тогда проведенные операции можно записать так:

Будем считать сначала, что определитель D1 основной матрицы системы (1) отличный от нуля. Тогда, как сказано выше,
, а потому, в крайнем случае, одно из чисел
(и=1, 2, ... , n) отлично от нуля, поскольку, если бы все были равны нулю, был бы равен нулю и определитель D2 основной матрицы системы (2).

Поскольку уравнения в системе (2) можно менять местами, поэтому, без ограничения, можно считать, что
. Поделим 2-е уравнение системы (2) на
, помножим полученную строку на (і=1, 3, 4, ... , n) и вычтем из і-й строки.

Тогда будем иметь

Система уравнений, что отвечает матрице В 3 , равнозначна системе (2), а поэтому и исходной системе (1). Определитель D3 основной матрицы этой системы отличный от нуля, поскольку отличный от нуля определитель D2. Отсюда, в крайнем случае, одно из чисел
(и=3, ... , n) отлично от нуля и можно снова провести те ж операции, что и ранее. Продолжая аналогичные размышления, после n операций получим матрицу

Соответствующая система уравнений имеет вид

(3),

Ее единственным решением есть (4)

Поскольку система (3) равнозначна системе (1), имеет единственное решение, то имеет единственное решение, что определяется формулами (4), и исходная система(1).

Пример 1 . Решить систему

Решение

x1=1; x2=-1; x3=0; x4=2

Отметим, если система однородна, то есть все числа bi (и=1, 2, ... , n) равны нулю, тогда равны нулю и все числа
Поэтому система (1) имеет в этом случае только нулевое решение.

Пусть теперь определитель D1 основной матрицы системы (1) равен нулю. Тогда уже нельзя утверждать, что среди чисел
(и=m, m+1, ... , n), полученных после (m-1)-го этапа преобразований, будет хотя бы одно, отличное от нуля. Больше того, на каком-то этапе все эти числа обязательно станут равными нулю (иначе мы имели бы разобранный случай). Таким образом, пусть получена матрица

Переставим m-ый столбец матрицы на место n-го, а все следующие за m-м столбцом, кроме столбца свободных членов
сдвинем на одно место влево (такая операция, очевидно, означает перестановку неизвестных в уравнениях системы или их перенумерацию, что, конечно, не изменяет решения системы). В результате получим матрицу

И=1, 2, ... , n;

k=m, m+1, ... , n.

Продолжая те ж преобразования, что и ранее, получим, в конечном счете, матрицу

(5)

Матрице (5) отвечает система уравнений

(6),

в которой неизвестные отличаются от неизвестных х і в системе (1) лишь нумерацией. Поскольку система (6) равнозначна системе (1), тогда вывод о решении системы (1) равносильный выводу о решении системы (6).

Очевидно, что если хотя бы одно из чисел
(и=k+1, ... , n) не равно нулю, тогда уравнение системы (6), а потому и уравнение системы (1), несовместимы. Если есть все (і=k+1, ... , n) равны нулю, тогда уравнения совместны. При этом неизвестным
можно дать любые значения, и система имеет такие решения:

где t1, t2, ... , te ( =n-k) произвольные

Для того, чтобы было удобно возвращаться к исходной системе неизвестных, полезно над столбцами матриц, которые получаются при проведении преобразований, надписывать обозначения соответствующих неизвестных. Укажем, кроме того, что если исходная система (1) однородна, тогда все числа (и=1, 2, ... , n) равны нулю. Поэтому имеют место такие два утверждения.

1. Система однородных уравнений 1-ого порядка всегда совместна.

2. Если определитель системы однородных уравнений 1-ого порядка равен нулю, тогда система имеет бесконечное множество решений.

Пример 2

Решение

Система уравнений, что отвечает полученной матрице, имеет вид:

Система совместна, х4=t произвольно. Система имеет бесконечное множество решений

причем t - произвольное число.

Отметим, что если бы свободные члены в уравнениях были другими, чем задано в условии, система могла бы быть несовместимой. Пусть, например, b4=1. Тогда преобразованная матрица системы будет

и последнее уравнение системы приобретет такой вид 0х1+0х2+0х3+0х4=1, что не имеет смысла.

Пример 3.

Решение.

Система совместима, х2=t произвольно; x1=1-t, x2=t, x3=-2, x4=1.

Разобранный метод без каких-либо изменений переносится и на тот случай, когда число неизвестных не совпадает с числом уравнений.

ІІ. Примеры решения задач

1.20. Решить систему

Вычислим определитель системы

Поскольку определитель системы отличный от нуля, применим правило Крамера. Для вычисления определителя detB1 заменим столбец определителя системы столбцом из свободных членов
. Имеем

Определитель detB2 получим заменой столбца
определителя системы столбцом из свободных членов:

Согласно правила Крамера, находим
;

Совокупность чисел (5;-4) является единственным решением данной системы.

1.21. Найти решения системы

Определитель из коэффициентов системы отличный от нуля:

detA=
=2·3·(-5)+5·(-9) ·2+(-8) ·4·3-(-8) ·3·2-5·4·(-5)-2·3·(-9)=-140

Поэтому можно применить правило Крамера

отсюда находим
;
;

Совокупность чисел (3, 2, 1) является единственным решением системы.

1.22. Решить систему

/IVp+II-I-III/ ~

Нетрудно видеть, что определитель из коэффициентов системы равен нулю, поскольку 4-ая строка его состоит из нулей. Последняя строка расширенной матрицы свидетельствует о том, что система не совместна.

1.23. Решить систему

Выпишем расширенную матрицу системы

/IIp. -2· I, IIIp. -I, IVp. -II-III/ ~
~

/поделим ІІІр. на (-3), IVp. на (-3)/

~
/ІІІр. +2· ІІ/ ~

В результате всех преобразований данная система линейных уравнений свелась к треугольному виду.

Она имеет единственное решение.

х3=1 х4=-1 х2=-2 х1=2 ▲

Уравнения совместимы, х4=t произвольно,

1.25. Найти решения системы

Система совместна, х4=t произвольно,

1.26. Решить систему

Система совместима, х4=t произвольно, x1=t, x2=-2t, x3=0, x4=t. ▲
^

§6 Ранг матрицы, теорема о совместимости систем уравнений первого порядка

Для исследования многих вопросов, связанных с решением систем уравнений 1-ого порядка, часто вводят понятие ранг матрицы.

Определение. Рангом матрицы называется самый высокий порядок отличного от нуля определителя квадратной субматрицы, полученной из заданной матрицы вычеркиванием некоторых строк и столбцов.

Рассмотрим, например, матрицу

Вычеркиванием любого числа строк и столбцов невозможно из заданной матрицы получить квадратную матрицу порядка выше 3-го. Отсюда, ранг ее не может быть больше трех. Но, вычеркивая один из столбцов, мы будем получать квадратные матрицы, которые имеют две одинаковые строки, а потому их определители равны нулю. Отсюда, ранг исходной матрицы меньше 3-х. Вычеркнув, например, 3-й и 4-й столбец и 3-й строку, получим квадратную матрицу
, определитель которой не равен нулю. Таким образом, все определители субматрицы 3-го порядка равны нулю, но среди определителей матриц 2-го порядка есть отличный от нуля. Тем самым ранг исходной матрицы равен двум.

Докажем теорему: ранг матрицы не изменяется при линейных операциях с ее строками.

Действительно, линейные операции со строками какой-либо матрицы приводят к тем же линейным операциям со строками любой субматрицы. Но, как указано выше, при линейных операциях со строками квадратных матриц определители этих матриц получаются один из другого умножением на число, отличное от нуля. Отсюда, нулевой определитель остается нулевым, а отличный от нуля - отличным от нуля, то есть не может измениться наивысший порядок отличного от нуля определителя субматриц. Не влияет, очевидно, на ранг матрицы и перестановка столбцов, поскольку такая перестановка может влиять лишь на знак соответствующих определителей.

Из доказанной теоремы выходит, что рассмотренные в предыдущем параграфе преобразованные матрицы имеют тот же ранг, что и исходные. Поэтому ранг основной матрицы системы уравнений первого порядка равен числу единиц на главной диагонали преобразованной матрицы.

Докажем теперь теорему про совместимость систем уравнений 1-ого порядка (теорема Кронекера-Капелли): для того чтобы система уравнений 1-ого порядка была совместима, необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы.

Пусть ранг основной матрицы системы равен k. Если ранг расширенной матрицы системы также равен k, тогда это означает, что или система содержит только k уравнений, или - все числа
(i= k+1, ... , k) в преобразованной матрице равны нулю (в противном случае ранг расширенной матрицы преобразованной, а потому и исходной системы был бы k +1)

Пусть ранг превращенной (а потому и исходной) расширенной матрицы системы больше k, то есть больше, чем число единиц на главной диагонали преобразованной матрицы. Тогда существует хотя бы одна субматрица (k+1)-го порядка, определитель которой не равен нулю. Такая субматрица может быть получена только прибавлением к единичной матрице порядка k (что находится в левом верхнем углу превращенной матрицы) какой-то одной строки и столбца, который состоит из первых k свободных членов уравнений преобразованной системы и любого одного свободного члена из следующих n-k уравнений. Чтобы определитель указанной субматрицы был отличный от нуля, отличным от нуля должен быть и этот последний добавленный элемент, то есть число (i=k+1, ... , k). Но, как было доказано ранее, в этом случае
система несовместима. Следовательно, система совместима тогда и только тогда, когда ранг основной матрицы совпадает с рангом расширенной матрицы.

ІІ. Примеры решения задач

1.39. Вычислить ранг матрицы с помощью элементарных преобразований

Где знак указывает, что соединенные ним матрицы получаются одна из другой элементарными преобразованиями, а потому имеют один и тот же ранг.

Ранг матрицы А равен 2, то есть r=2. ^

1.40. С помощью элементарных преобразований вычислить ранг матрицы

r=3, т.к. определитель треугольной матрицы с первых трех столбцов не равен нулю. ▲

Вычисление рангу матрицы методом обрамления

Выбираем в данной матрице минор второго порядка, отличный от нуля. Потом вычисляем миноры третьего порядка, которые обрамляют (включают в себя) выбранный, пока не найдем среди них отличного от нуля. Дальше вычисляем миноры четвертого порядка, которые обрамляют отличный от нуля минор ІІІ-го порядка, пока не найдем среди них отличный от нуля, и т.д. Если найти отличный от нуля минор r-го порядка, а все обрамляющие его миноры (r+1)-го порядка равны нулю или их уже нет, то ранг матрицы равен r.

1.41. Вычислить ранг матрицы

∆
Вычеркнули ІІІр. , поскольку 2·ІІр. +І естьІІІр.

Выберем, например,

Вычислим миноры ІІІ-го порядка, которые обрамляют его

минор ІІІ-го порядка отличный от нуля.

Он содержится в определителе IV порядка заданной матрицы, который равен нулю. Следовательно, r=3. ▲

1.42. Решить системы уравнений

а) Здесь r(A)=3, r(B)=3; система совместимая, определенная.

Поскольку
,

тогда из первых трех систем, например, согласно формул Крамера, находим

х1=-1, х2=0, х3=1

b) Здесь r(A)=2, r(B)=2; система совместима, но не определенная.

Определитель

и из первых двух уравнений системы

где неизвестным х3 и х4 можно давать любые значения.

в) в этом случае r(A)=2, r(B)=3; и система несовместима.

1.43. Методом Гаусса (последовательного исключения неизвестных) решить однородную систему уравнений:

и найти ее фундаментальную систему решений.

Выпишем расширенную матрицу системы (при этом нулевой столбец можно, конечно, не писать). После понятных преобразований будем иметь

то есть заданная система равнозначна следующей:

Здесь r=3, и три неизвестных можно выразить через последние, например, так:

х 2 =-2х 3 -3х 4 -9х 5 =-2х 3 -12х 5

х 1 =-2х 2 -3х 3 -4х 4 -5х 5 =х 3 +15х 5

Фундаментальную систему можно получить, если свободным неизвестным х3, х5 придавать значение х3=1, х5=0 (тогда х1=1, х2=-2, х4=0) и значение х3=0, х5=1 (тогда х1=15, х2=-12, х4=1). Это дает фундаментальную систему решений:

e 1 =(1, -2, 1, 0, 0), e 2 =(15, -12, 0, 1, 1)

С использованием фундаментальной системы часто записывают общее решение в виде линейной комбинации решений е 1 та е 2 , то есть:

1.44. Найти фундаментальную систему решений системы линейных уравнений и записать ее общее решение

Третью строку отбросим. Система свелась к ступенчатой с основніми неизвестными х1, х2 и свободными х3, х4:

Из последнего уравнения
. Из первого
Свободных неизвестных 2. Поэтому берем определитель ІІ порядка с единичными элементами главной диагонали и нулевыми - побочной:
.

Получим вектор e 1 = (
)

Векторы e 1 и e представляют собой фундаментальную систему решений.

Теперь общее решение можно записать в виде

Присваивая коэффициентам , любые (произвольные) числовые значения будем получать разнообразные частичные решения.

/из всех строк вычтем IV/

II, III, V строки, которые пропорциональны к І-й, вычеркнем. В полученной матрице переставим І и ІІ столбцы:

Ранг матрицы равен 2.

Основные неизвестные х2 и х1. Свободные - х3, х4, х5. Система теперь имеет вид:

Присваивая свободным неизвестным последовательно значения, которое равны элементам столбцов определителя

1) х3=1, х4=0, х5=0; 2) х3=0, х4=1, х5=0; 3) х3=0, х4=0, х5=1

1) х2=1, х1=1; 2) х2=1, х1=-2; 3) х2=-2, х1=1

то есть векторы С 1 =(1, 2, 1, 0, 0)

С 2 =(-2, 1, 0, 1, 0)

С 3 =(1, -2, 0, 0, 1)

составляют фундаментальную систему решений. Общее решение системы теперь останется.

Матрица коэффициентов

имеет ранг r=2 (проверьте).

Выберем за базисный минор

Тогда сокращенная система имеет вид:

Откуда, считая х3=с1, х4=с2, х5=с3, находим

Общее решение системы

Из общего решения находим фундаментальную систему решений

С использованием фундаментальной системы общее решение может быть записано

e=с1e1+с2e2+с3e3
^

§7 Основные операции с матрицами

В предыдущем параграфе широко применялись линейные операции со строками и столбцами различных матриц. Но в некоторых вопросах линейной алгебры приходится рассматривать операции с матрицами как с единым объектом.

В основе изучения операций с матрицами лежит понятие равенства матриц. Будем исходить из такого определения : две матрицы одной и той ж размерности называются равными, если равны все их соответствующие элементы.

Следовательно, матрицы А і В одной и той же размерности nxm равны тогда и только тогда, когда Aik=Bik i=1, 2,... , n; k=1, 2,... , m. При этом еще раз подчеркнем, что сравнивать можно лишь матрицы одной и той же размерности.

Суммой двух матриц А и В одной и той же размерности nxm называется матрица С той же размерности такая, что

(С) ik =(A) ik +(B) ik (1)

Следовательно, при прибавлении матриц (прибавлять можно только матрицы одной и той же размерности) надо складывать все их соответствующие элементы.

Поскольку прибавление матриц сводится к прибавлению чисел - элементов этих матриц, очевидно, имеет место коммутативное и ассоциативное свойство.

А+В=В+А; (А+В)+С=А+(В+С) (2)

Произведением матрицы А на число  (или числа  на матрицу А) называется матрица В такая, что

(В) ik =(A) ik (3),

то есть при умножении матрицы на число (или числа на матрицу) необходимо все элементы матрицы умножить на это число. Напомним, что при умножении на число определителя матрицы достаточно было умножить на это число лишь элементы любой строки (или столбца).

Легко проверить, что при умножении матрицы на число имеет место распределительное свойство:

(А+В)=А+В; (+)=А+В (4)

Определим теперь произведение двух матриц. Пусть дана матрица А размерности nxm и матрица В размерности mxp.

Определение. Произведением матрицы А размерности nxm на матрицу В размерности mxp называется матрица С размерности nxp такая, что

(5),

иначе говоря, для получения элемента, что находится в і-й строке и в k-ом столбцу матрицы произведения, нужно вычислить сумму произведений элементов і-й строки первого множителя и соответствующих элементов k-го столбца второго множителя. Следовательно, для того чтобы возможно было сложить указанную сумму, нужно равенство числа столбцов в первой матрице (то есть число элементов в каждой строке) числу строк в другой (то есть числу элементов в каждом столбце).

Пример 1.

Найти АВ

Решение. Матрица А имеет размерность 3х2, матрица В 2х2; произведение существует - это матрица размерности 3х2.

Произведение матриц не имеет переставного свойства: АВ, вообще говоря, не равно ВА.

Во-первых, из того, что можно вычислить АВ, совсем не выходит, что имеет смысл ВА. Например, в только что разобранном примере перестановка множителей, то есть умножение В на А невозможно, поскольку нельзя матрицу размерности 2х2 умножить на матрицу размерностью 3х2 - число столбцов первой матрицы здесь не равно числу строк другой. Но даже если произведение ВА существует, то нередко
. Рассмотрим пример.

Пусть
. Тогда

Вместе с тем, можно доказать (такое доказательство мы рекомендуем провести читателю), что

(АВ)С=А(ВС) (6)

А(В+С)=АВ+АС

(обычно принимается к вниманию, что все эти произведения имеют смысл).

В соответствии с определением произведения матриц всегда возможно умножение квадратных матриц одного порядка, при этом произведение будет матрицей того же порядка. Отметим без доказательства одно из свойств произведения квадратных матриц одного порядка: определитель произведения двух матриц одного и того же порядка равен произведению определителей матриц, которые перемножаются.

Очень часто приходится рассматривать произведение матрицы размерности nxm на матрицу размерности mx1, то есть на матрицу с одним столбцом. Очевидно, мы должны получить в результате матрицу размерности nx1, то есть также матрицу с одним столбцом. Пусть, например, необходимо умножить матрицу

на матрицу

В результате получим матрицу
, элементы которой исчисляются по формулам:

Но это означает, что систему уравнений 1-ого порядка, рассмотренную в предыдущем параграфе, можно записать в очень удобной матричной форме: АХ=В.

Существенную роль в различных применениях матричной алгебры играет квадратная матрица, у которой все диагональные элементы (то есть элементы, которые находятся на главной диагонали) равны 1, а все другие элементы равны нулю. Такая матрица называется единичной матрицей. Очевидно, что определитель единичной матрицы

= 1

Характерны следующие свойства единичной матрицы: пусть задана квадратная матрица А порядка n и Е-единичная матрица того же порядка. Тогда АЕ=ЕА=А.

Действительно
, но

Поэтому в сумме
отличные от нуля только те составные, для которых e=k. Следовательно, (АЕ) ік =(А) ік, и отсюда АЕ=А. Аналогично получаем и для произведения ЕА.

Примеры решения задач

1.61. Найти произведение АВ и ВА двух матриц

∆ Произведение АВ не существует, так как число столбцов матрицы А не равно числу строк матрицы В. Число столбцов матрицы В равно числу строк матрицы А. Следовательно существует произведение ВА:

1.62. Найти матрицу 2А+5В, если

Системой m линейных уравнений с n неизвестными называется система вида

где a ij и b i (i =1,…,m ; b =1,…,n ) – некоторые известные числа, а x 1 ,…,x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы .

Числа, стоящие в правых частях уравнений, b 1 ,…,b m называются свободными членами.

Совокупность n чисел c 1 ,…,c n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c 1 ,…,c n вместо соответствующих неизвестных x 1 ,…,x n .

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной . В противном случае, т.е. если система не имеет решений, то она называется несовместной .

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

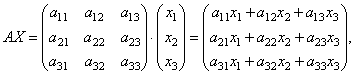
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

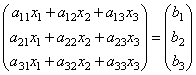или короче A ∙X=B .

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением .

Пусть определитель матрицы отличен от нуля |A | ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A : . Поскольку A -1 A = E и E ∙X = X , то получаем решение матричного уравнения в виде X = A -1 B .

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных . Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B .

Примеры. Решить системы уравнений.

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы .

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство . Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A 11 элемента a 11 , 2-ое уравнение – на A 21 и 3-е – на A 31 :

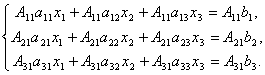
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x 1 . Для этого второе уравнение разделим на а 21 и умножим на –а 11 , а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а 31 и умножим на –а 11 , а затем сложим с первым. В результате исходная система примет вид:

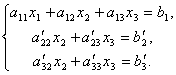
Теперь из последнего уравнения исключим слагаемое, содержащее x 2 . Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x 3 , затем из 2-го уравнения x 2 и, наконец, из 1-го – x 1 .

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

Таким образом, система имеет бесконечное множество решений.

Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.
2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение . Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Пример №1:

Решим методом подстановки

Решение системы уравнений методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y.Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Пример №2:

Решим методом почленного сложения (вычитания).

Решение системы уравнений методом сложения

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2

5y=32 | :5
y=6,4

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно . Без шуток.

1. Метод подстановки : из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.

Задача. Решить систему уравнений:

Решение. Из первого уравнения системы выражаем у через х и подставляем во второе уравнение системы. Получим систему равносильную исходной.

После приведения подобных членов система примет вид:

Из второго уравнения находим: . Подставив это значение в уравнение у = 2 - 2х , получим у = 3. Следовательно, решением данной системы является пара чисел .

2. Метод алгебраического сложения : путем сложения двух уравнений получить уравнение с одной переменной.

Задача. Решить систему уравнение:

Решение. Умножив обе части второго уравнения на 2, получим систему равносильную исходной. Сложив два уравнения этой системы, придем к системе

После приведения подобных членов данная система примет вид: Из второго уравнения находим . Подставив это значение в уравнение 3х + 4у = 5, получим , откуда . Следовательно, решением данной системы является пара чисел .

3. Метод введения новых переменных : ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.

Задача. Решить систему уравнений: