hibamérés
A mérési eredmény eltérése a mért érték valódi (érvényes) értékétől.
Szinonim kifejezés mérési hiba a kifejezés mérési hibamelyik felhasználás nem ajánlott kevésbé sikeresnek
A mérési eredmény összetett hibája, állandó vagy állandóan változó, ugyanazon fizikai mennyiség ismételt mérésével.
Megjegyzés - A mérés jellegétől függően a szisztematikus hibák oszthatók állandó, progresszív, időszakos és bonyolult jogi hibák.
Állandó hibák - hibák, amelyek hosszú ideig megtartják értéküket, például a teljes mérési sorozat végrehajtási ideje alatt. Ezek a leggyakoribbak.
Progresszív hibák - folyamatosan növekvő vagy csökkenő hibák. Ezek közé tartoznak például a mérőcsúcsok elhasználódásából adódó hibák, amelyek az aktív részegységgel érintkeznek, amikor egy aktív vezérlőeszköz vezérli.
Az időszakos hibák olyan hibák, amelyek értéke az idő periodikus függvénye vagy a mérőműszer mutatójának mozgása.
A bonyolult jog szerint változó hibák több szisztematikus hiba közös fellépésének eredményeként következnek be.
A mérési hiba összetevője az alkalmazott mérőműszer hibája miatt
módszer hiba
Az elfogadott mérési módszer tökéletlensége által okozott szisztematikus mérési hiba összetevője.
jegyzetek
1 A mérések egyenletei által elfogadott egyszerűsítések miatt gyakran jelentős hibák állnak rendelkezésre annak érdekében, hogy ellensúlyozzák azokat a lépéseket, amelyek korrekcióit be kell vezetni. A módszer hibáját néha hívják elméleti hiba.
2 Néha a módszer hibája véletlenszerűnek tűnhet.
A szisztematikus mérési hiba összetevője, amely az eltérés egyik, a mérési körülményeket jellemző paraméterek egyik irányába történő el nem számolt hatásának következménye.
Megjegyzés - Ezt a kifejezést nem számolt vagy nem megfelelő módon figyelembe veszik egy bizonyos befolyásoló érték (hőmérséklet, légköri nyomás, levegő páratartalma, mágneses térerősség, rezgés stb.) Esetében; a mérőműszerek helytelen telepítése, a kölcsönös elrendezés szabályainak megsértése stb.
szubjektív hiba
A szisztematikus mérési hiba az üzemeltető egyedi jellemzői miatt.
jegyzetek
1 Vannak olyan szereplők, akik rendszeresen késnek (vagy előre) a mérőműszerek leolvasására.
2 Néha szubjektív hibát hívnak személyes hiba vagy személyes különbség
NSP
A mérési eredmény összetett hibája a rendszerszintű hibák vagy a szisztematikus hibák befolyásolására vonatkozó módosítások számításai és bevezetése miatt bekövetkezett hibák miatt;
véletlen hiba
A mérési eredmény összetett hibája, véletlenszerűen változó (jel és érték) az azonos gondossággal végzett ismételt mérések során, ugyanaz a fizikai mennyiség
abszolút hiba
A mérési hiba mértékegységben kifejezve
Hibaérték a jelének figyelembevétele nélkül (hiba modulus)
Megjegyzés - Meg kell különböztetni a kifejezéseket. abszolút hiba és a hiba abszolút értéke
relatív hiba
A mérési hiba az abszolút mérési hiba és a mért érték tényleges vagy mért értékének arányában kifejezve.
szórási eredmények;
szóródás
Az egyenlő mértékű mérések sorozatában kapott mérések eredményei közötti eltérés általában véletlenszerű hibák hatására következik be.
jegyzetek
1 A véletlenszerű hibák következményeiből adódóan a mérési sorozatokban az eredmények diszperziójának mennyiségi becslését általában a szisztematikus hibák hatására vonatkozó korrekciók bevezetése után kapjuk meg.
2 A mérések sorozatának szóródásának becslése lehet:
körét,
aritmetikai átlagos hiba (modulonként),
standard hiba vagy szórás (standard eltérés, kísérleti szórás), \\ t
a hiba megbízhatósági határai (bizalmi határ vagy bizalmi hiba)
söprés
értékelés Egy sorozat (vagy egy minta) fizikai mennyiségének egyetlen mérése eredményeinek szórása n mérések), a képlettel számítva
Rn = X max - X min
ahol X max és X min - a fizikai mennyiség legnagyobb és legkisebb értékei ebben a mérési sorozatban.
Megjegyzés - A szórás általában a véletlenszerű okok előfordulásának köszönhető, és a természetben valószínű.
átlagos négyzetmérési hiba;
átlagos négyzethiba;
UPC
Az egyetlen mérés szórásának becslése egyenlő mérések sorozatát eredményezi ugyanazon fizikai mennyiségek átlagértéke körül
ahol xi az i-edik egységmérés eredménye;
X az n egyetlen eredmény mért értékének számtani átlaga.
MEGJEGYZÉS A gyakorlatban a kifejezés széles körben elterjedt. átlagos négyzet eltérés - (SKO). A (9.6) képlet szerinti eltérést úgy értjük, hogy az egyedi eredmények egy mérési sorozatban eltérnek számtani átlagértéküktől. A metrológiában, amint azt a 9.1. Ha a mérési eredményeket a szisztematikus hibák hatására korrigálják, akkor az eltérések véletlenszerű hibák. Ezért a kifejezések összességének egyszerűsítése szempontjából, az általános kifejezés, amely a „mérési hiba” kifejezés, célszerű az „átlagos négyzethiba” kifejezést használni. A szisztematikus hibáktól mentes mérési eredmények sorozatának feldolgozása során az EUC és az EQ ugyanaz a becslés az egyes mérések eredményeinek szóródására.
az aritmetikai átlag négyzethibája;
közepesnégyzetes hiba;
UPC
értékelésS x az adott mérési sorozaton azonos értékű mérési eredmény számtani középértékének véletlen hibája, a képlettel számítva
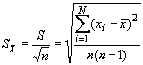
, (9.7)
ahol S az egyenlő mérések sorozatából kapott egyedi mérések eredményeinek átlagos négyzetes hibája; n az egyes mérések száma a sorozatban
a hiba bizalmi határai;
bizalmi határok
A mérési hiba legnagyobb és legkisebb értéke, amely korlátozza azt az intervallumot, amelyen belül a mérési eredmény hiba kívánt (valós) értéke egy adott valószínűségen belül van.
2 Szimmetrikus határok esetén a kifejezést a szingulárisan lehet használni. bizalmi határ.
3 Néha a kifejezés helyett bizalmi határ használja a kifejezést bizalmi hiba vagyhiba egy adott megbízhatósági szinten
9.17 javítás
A nem korrigált mérési eredményben megadott értékérték a szisztematikus hiba összetevőinek kiküszöbölése érdekében.
Megjegyzés - A módosítás jele ellentétes a hiba jelével. Az intézkedés névértékéhez hozzáadott módosítást hívják érték módosítására; a mérőleolvasásban bevezetett módosítást hívjákaz eszköz olvasatának módosítása
9. 18 korrekciós tényező
A szisztematikus hiba hatásának kiküszöbölése érdekében a nem korrigált mérési eredmény szorzata.
Megjegyzés - A korrekciós tényezőt olyan esetekben használják, amikor a rendszeres hiba arányos az értékkel
9. 19 a mérési eredmény pontossága;
mérési pontosság
A mérési minőség egyik jellemzője, amely a mérési eredmény hibájának közelségét tükrözi.
Megjegyzés - Vegyük figyelembe, hogy minél kisebb a mérési hiba, annál nagyobb a pontossága
9 . 20 bizonytalanság mérés;
bizonytalanság
A mérési eredményhez társított paraméter, amely a mért értékhez tartozó értékek szórását jellemzi.
jegyzetek
1 Meghatározás a VIM-93-ból.
2 A megjegyzésekben szereplő meghatározás szerepel, amelyből következik:
a) egy paraméter lehet egy standard szórás (vagy annak többszörösére), vagy a megadott konfidenciaszintű intervallum felére;
b) a bizonytalanság (többnyire) sok összetevőből áll. Ezek közül az összetevők közül néhányat a statisztikailag elosztott mérési sorozatban kísérleti standard deviációval lehet becsülni. Más összetevők, amelyek standard eltérésekkel is becsülhetők, kísérleti adatokon vagy egyéb információkon alapulnak.
9. 21 kalibrációs módszer hiba
A készülék méretének a kalibrálás során történő átvitelére alkalmazott módszer pontossága
9. 22 érettségi mérési hiba;
érettségi hiba
A mérőműszer skálájának egy vagy másik jeléhez rendelt érték valós értékének hibája az érettségi következtében
9. 23 hiba visszajátszás fizikai mennyiség egységei;
reprodukciós hiba
A fizikai mennyiség egységének reprodukálásakor elvégzett mérési eredmények hibája.
Megjegyzés - Az egységnek az állami szabványok segítségével történő reprodukálásának hibája általában összetevőinek formájában jelenik meg: nem kizárt rendszeres hiba; véletlen hiba; az év instabilitása
9. 24 a fizikai mennyiség egységének átadásának hibája;
egységméret hiba
A mérési eredmény hibája az egység méretének átvitele során.
Megjegyzés - Az egység méretének átvitelében bekövetkező hiba magában foglalja a módszer és a mérőműszerek nem kizárt rendszeres és véletlen hibáit is
9. 25 statikus mérési hiba;
statikus hiba
A statikus mérési körülményekhez tartozó mérési hiba
9. 26 dinamikus mérési hiba;
dinamikus hiba
Mérési hiba a dinamikus mérési körülmények között
9. 27 csúszás
Az egy mérés eredményének hibája, amely egy méréssorozatban szerepel, amely ezekre a körülményekre jelentősen eltér a sorozat többi eredményétől.
Megjegyzés - Néha a „miss” kifejezést használják helyett bruttó hiba mérési
9. 28 mérési hiba egy méréssorozatban;
hibahatár
Ehhez a mérési feladathoz engedélyezett maximális mérési hiba (plusz, mínusz).
9. 29 egyetlen mérés eredményének hibája;
mérési hiba
Egy mérés hibája (nem része a mérések sorozatának), amelyet a mérőeszközök és a mérési mód ismert hibáinak alapján becsülnek meg ezekben a körülményekben (mérések).
Példa - Bármely részméret egyetlen mikrométeres mérése 12,55 mm értéket eredményez. Ugyanakkor a mérés előtt ismert, hogy ebben a tartományban a mikrométer hiba ± 0,01 mm, és ebben az esetben a módszer hibája (közvetlen értékelés) nulla. Ezért az eredmény hibája ± 0,01 mm lesz az adott mérési körülmények között
9. 30 a mérési eredmény teljes átlagos négyzetes hibája;
az eredmény teljes hibája;
teljes hiba
A mérési eredmény hibája (véletlenszerűen véletlenszerű és nem kizárt szisztematikus hibák összegéből áll), a képlet alapján számítva
, (9.8)
ahol
Az egyenletes eloszlású (véletlenszerűnek tekintett) nem kizárt szisztematikus hibák összegének átlagos négyzetes hibája.
Megjegyzés - A teljes hiba megbízhatósági határértékei (Δx) Σ kiszámítható a képlettel
( Δx) Σ = ± t Σ S Σ (9.9)
ahol; Θ - a mérési eredmény nem kizárt rendszerszintű hibáinak összege, a (9.2) vagy (9.3) képlettel számítva; t * Sx - a mérési eredmény hibájának 9.16
Töltési idő
6,5 és 8,5 V között
2.4 A földfelszínen lévő pontok pozíciójának meghatározása geodéziai műholdrendszerek segítségével
Az oroszországi térképészeti szövetségi geodézia által kidolgozott, topográfiai és geodéziai termelés műholdas koordináta-definíciók autonóm módszereihez történő átadásának koncepcióját és programját bemutatja az E. A. Zhalkovsky, G. V. Demyanova, V. Zubinsky, P. L. Makarenko, G. A. Pyankova, "A topográfiai és geodéziai termelésnek a műholdas koordináta-meghatározás autonóm módszereire történő átadásának koncepciójáról és programjáról" (Geodesy and Cartography, 1998, No. 5). A hagyományos geodéziai módszerek a geodéziai hálózatok szögletes és lineáris méréseken alapuló következetes fejlesztésén alapulnak, amelyek a közvetlen szomszédos geodéziai jelek közötti láthatóságot teszik szükségessé, amelynek építése a meglévő referenciahálózatok létrehozására fordított források mintegy 80% -át igényli.
A hagyományos műholdas módszerekhez képest GLONASS / GPS az alábbi előnyökkel jár:
nagyfokú hatékonysággal és koordinátákkal való pontosságú átvitel szinte bármilyen távolságra;
a geodéziai pontok a biztonságuk szempontjából kedvező helyeken helyezkednek el, mivel nem szükséges kölcsönös láthatóságot biztosítani a pontok között, és ezért drága geodéziai jeleket kell kialakítani;
az egyszerűség és a magas szintű automatizálás;
az eredeti geodéziai alap sűrűségi követelményeinek csökkentése.
A műholdas technológia bevezetése a következő geodéziai hálózatok építését foglalja magában:
az alapvető asztronómiai-geodéziai hálózat (FAGS) a legmagasabb szintű koordináta-támogatás; biztosítani kell az általános geocentrikus koordinátarendszer gyors helyreállítását, a koordinátarendszer stabilitását időben, metrológiai, nagy pontosságú térmérő eszközök biztosítását;
nagy pontosságú geodéziai hálózat (HCV), amely biztosítja az általános geocentrikus koordinátarendszer terjesztését és az általános geodéziai és referencia-koordinátarendszerek relatív tájolásának pontos paramétereit az ország egész területén;
1. osztályú műholdas geodéziai hálózatok (SGS-1).
Ez a három hálózati osztály szigorúan összekapcsolódik: a FAGS a HCG alapja, a HCV pedig a GHS-1 esetében.
A FAGS, a VGS és a GHS-1 építésekor a meglévő GGS a legmagasabb szintű műholdas hálózatokhoz kapcsolódik, azaz a meglévő GGS egy sűrűző hálózat lesz.
A FAGS pontjai 800-1000 km távolságban vannak, számuk - 50 + 70,10-15 pontot kell tartósan működtetni, és a többit csoportokban időközönként újra kell definiálni a régió geodinamikai aktivitásától függően.
A FAGS-pontok térbeli helyzetét az általános föld koordinátarendszerben határozzák meg, a pontok helyzetének hibája legfeljebb (2-3) 10-8 R, ahol R a Föld sugara, a FAGS relatív helyzetének hibája nem haladja meg a 2 cm-t és 3 cm-t. . Ennek a pontosságnak a biztosítása érdekében a meglévő térmérések teljes skáláját kell használni (lézer, rádióinterferometriai és mások).
A HCV olyan pontrendszer, amely között D = 150-300 km távolság van, amelyet a térbeli geodézia viszonylagos módszerei határozzák meg, a tervezett koordinátáknál 3 mm + 5 10-8 D-nál kisebb standard hiba esetén, és 5 mm + 7 10-8 D geodéziai méréseknél. magasságokba.
A GHS-1 egy könnyen hozzáférhető pontrendszerből áll, amelynek sűrűsége elegendő ahhoz, hogy a fogyasztók mindenféle műholdas meghatározást használjanak. A GHS-1-et a térbeli geodézia viszonylagos módszerei határozzák meg: 3 mm + 10-7 D tervben és 5 mm + + 2 10-8 D a geodinamikai szempontból aktív területek geodéziai magassága és 5 mm + 2 10-7 között. D a tervben és 7 mm + 3 10-7 D magasságban a többi régióban. A GHS-1 pontok közötti átlagos távolság 25-35 km. Gazdaságilag fejlett területeken az SGS-1 pontok a fogyasztók igényeitől függően nagyobb sűrűséggel rendelkezhetnek.
A tartósan működő FAGS-pontokat főként a műholdas (űr) megfigyelések, csillagászati megfigyelők, földi rotációs pontok, rádióinterferometriás komplexek ultra hosszú Kvazar bázisokkal, a Delta programmal és másokkal kapcsolatos működési pontjai alapján állítják elő. műholdas felügyeleti rendszerek GLONASSés GPS (beleértve a nemzetközi programokat) és más speciális műholdak és űrobjektumok megfigyelései a FAGS építésének ügynökségközi programjai szerint.
Meg kell jegyezni, hogy a műholdas technológiák nem mindig használhatók a hagyományos geodéziai feladatok megoldására, például a rövid távolságokra vonatkozó definíciók relatív pontossága nem elegendő, a GPS-módszerek használata pontos mérnöki felmérésa hagyományos technológiában könnyen megoldható kötési referenciapontok folyamata meglehetősen bonyolultnak és drágává válik, különösen zárt területeken, a műholdas technológiában, mivel ebben az esetben a műholdas meghatározások mennyisége meghaladja a kétszeresét.
3. A geodéziai mérések hibája (a problémák elmélete és megoldása)
3.1 Geodéziai mérés, mérési eredmény, mérési módszerek és feltételek. Egyenlő és nem lineáris mérések
A mérés az egyes fizikai mennyiségek azonos nevű értékkel való összehasonlításának mértékét jelenti.
A mértékegység az egyfajta érték számszerűsítéséhez használt fizikai mennyiség értéke.
A mérési eredmény egy szám, amely megegyezik a mértékegység mért értékének arányával.
A következő típusú geodéziai mérések léteznek:
Ennek eredményeként lineáris, amely ferde, irracionális távolságot kap az adott pontok között. Erre a célra szalagok, mérőszalagok, vezetékek, optikai fény és rádió távolságmérők kerülnek alkalmazásra.
Szög, meghatározva a vízszintes szögek nagyságát. Az ilyen mérések elvégzése teodolit, iránytű, ekliméter segítségével.
Magasság, ami az egyes pontok magasságának különbségét kapja. Ebből a célból felhasználási szintek, teodolit-tacheométerek, barométerek.
A geodéziai méréseknek két módja van: közvetlen és középszerű (közvetett).
Közvetlen mérések, amelyekben a meghatározott értékeket a mérési egységgel való közvetlen összehasonlítás eredményezi.
Közvetett mérések, amelyekben a meghatározott értékeket más közvetlenül mért értékek függvényeként kapjuk meg.
A mérési folyamat a következőket tartalmazza:
Objektum - amelynek tulajdonságai, például a mérete jellemzi a mérési eredményt.
Technikai eszközök - az eredmény elérése a megadott egységekben.
Mérési módszer - a gyakorlati intézkedések és a technikai eszközök technikája miatt.
Mérő - felvevő készülék
A külső környezet, amelyben a mérési folyamat.
A mérések megkülönböztetik az egyenlő és nem egyenlő értékeket. Egyenlő - ezek homogén mennyiségek mérésének eredményei, amelyeket ugyanazon osztályú műszerek segítségével végeztek, ugyanazon módszerrel, egy előadó által ugyanazon feltételek mellett. Ha a népességet alkotó elemek legalább egyike változik, akkor a mérési eredmény egyenlőtlen.
3.2 A geodéziai mérések hibáinak osztályozása. RMS hiba. Gauss és Bessel formái a számításhoz
A nagyon jó körülmények között elvégzett geodéziai mérések hibákat is okoznak, azaz az L mérési eredmény eltérése a számozott mennyiség X-es értékétől:
Az igaz egy olyan mérhető mennyiség értéke, amely ideálisan tükrözné egy objektum mennyiségi tulajdonságait. Az elérhetetlen feltétel - valódi érték - hipotetikus fogalom. Ez egy olyan érték, amely végtelenül közelíthető meg, nem érhető el.
Mérési pontosság - az eredmény közelítésének mértéke a valós értékhez. Minél alacsonyabb a hiba, annál nagyobb a pontosság.
Abszolút hiba a mért érték és a valódi nagyságmérés eredményeként kapott érték különbsége. Például, ha a tényleges érték l = 100 m, ugyanazon vonal mérésekor az eredmény 100,05 m, akkor az abszolút hiba:
E = Xszerkesztett – X
E = 100,05 - 100 = 0,05 (m)
Az érték megszerzéséhez elég egy mérés elvégzése. Ezt szükségesnek nevezik, de gyakrabban nem korlátozódik egy dimenzióra, hanem legalább két alkalommal megismétlik. Azokat a méréseket, amelyek túlmutatnak a szükségeseken, redundánsnak (kiegészítőnek) nevezzük, ezek a mérés eredményének nagyon fontos eszközei.
Az abszolút hiba nem ad képet az eredmény pontosságáról. Például 0,06 m-es hiba lehet az l = 100 m vagy l = 1000 m mérésével, ezért a relatív hibát kiszámítjuk:
C = Evö / X
C = 0,06 / 100 = 1/1667, azaz 1667 m-en mért 1 méteres hiba történt.
Relatív hiba - az abszolút hiba és a tényleges vagy mért érték aránya. Express frakció. Az utasítások szerint a terepvonalat nem szabad durvábbra mérni, mint 1/1000.
Az egyes tényezőkből eredő hibákat elemi névnek nevezik. Az általánosított hiba az elemi összeg összege.
Vannak:
durva (Q),
szisztematikus (o)
véletlenszerűen (∆).
durva A mérési hibák bruttó hibákból, a vállalkozó hibáiból, gondatlanságából, technikai eszközök észrevétlen hibáiból erednek. A durva hibák teljesen elfogadhatatlanok, és ismételt, további mérésekkel teljesen ki kell zárni a mérési eredményekből.
szisztematikus mérési hibák - a hibával kapcsolatos állandó összetevő: látás, műszaki eszközök meghibásodása, hőmérséklet. A szisztematikus hibák egyoldalúak és változóak lehetnek (időszakos hibák). Amikor csak lehetséges, munkájuk megszervezése és lebonyolítása során azokat a mérési eredményeket figyelembe veszik vagy kizárják.
véletlen a mérési hibák elkerülhetetlenül kísérik az összes mérést. A véletlenszerű hibák nem zárhatók ki, de a kívánt eredményre gyakorolt hatásuk további mérésekkel csökkenthető. Ezek az összes méréssel kapcsolatos legrosszabb hibák. Lehet, hogy a méret és a jelzés is különbözik.
Ha bruttó és szisztematikus hibákat lehet vizsgálni és kizárni a mérési eredményből, akkor a véletlenszerű hibákat mély mérés alapján lehet figyelembe venni. A valószínűségi elméleten alapuló tanulmány.
A gyakorlatban a nehézség abban rejlik, hogy a méréseket korlátozott számú alkalommal végezzük el, és ezért a mérések pontosságának becsléséhez a standard szórás becsült értékét kell megadni. rms hiba.
A Gauss-t az átlag négyzetes hibára vonatkozó képlet javasolta:
∆2cp = (∆21 + ∆22 +… + ∆2n) / n,
∆2 = m2 = (∆21 + ∆22 +… + ∆2n) / n,
∆vö = m = √(∑∆ 2 én / n)
A képletet akkor alkalmazzák, ha a hibákat a valós értékekből számítják ki.
Bessel-formula:
m = √(∑ V2 én / (n-1))
Az aritmetikai átlag átlagos négyzetes hibája n n-szer kisebb, mint az egyéni mérés átlagos négyzetes hibája.
M =m/ Cn
Becslésekor a pontossági mértékegységként az egynél nagyobb súlyú standard hibát alkalmazzák. A súlyegység átlagos négyzetes hibája.
µ 2 = PBm2 - µ = m√P, m = µ / √P, azaz a mérési eredmények átlagos négyzetes hibája megegyezik a mérési hibával, amelynek súlya 1 (µ), és osztva az eredmény (P) súlyának négyzetgyökével.
Kellően nagy számú méréshez ,m2P = ∑∆2P (∆ = m) óta írhatunk:
µ = √(∑(∆ 2 BP)/ n) Ie az 1-es egyenlő súlyú átlag négyzetmérési hiba megegyezik a számláló négyzetgyökével, amelynek súlya az egyenlőtlen dimenziós mérések abszolút hibahelyeinek termékeinek összege, és a nevezőben az egyenlőtlen dimenziós mérések száma.
A teljes aritmetikai átlag átlagos négyzetes hibája a következő képlettel:
M0 = µ / √∑ P
Az µ értékét helyettesítő µ:
M0 = √ (∑∆2ЧP / n) / (√∑P) = √ [(∑∆2ЧP) / nЧ (∑P)]
M0 = √[ (∆ 1 2 P1 + ∆ 2 2 P2 +… + ∆ n2 Pn) / nH (P1 + P2 + … + Pn) ] – képletgauss, a teljes aritmetikai átlag átlagos négyzetes hibája megegyezik a frakció négyzetgyökével, amelynek a számlálójában a nem egyenlő dimenziójú mérések hibáinak négyzeteinek összege a súlyukhoz, és a nevező a súlyuk összegeinek számának eredménye.
µ = √ [∑(V2 BP) / (n-1)] Ez az bessel-formula az aritmetikai átlaghiba kiszámítása 1-es súlyméréssel, a nem egyenlő mértékű mérések számában, a valószínű hibák alapján. Nagyszámú mérésre érvényes, és korlátozott (gyakran a gyakorlatban) hibákat tartalmaz: mµ = µ / a µ becslés megbízhatósága.
Teszt probléma 1
A teodolit tanulmányozására többször ugyanazt a szöget méri. Az eredmények a következők: 39˚17,4 "; 39˚16,8"; 39˚16,6 "; 39˚16,2"; 39˚15,5 "; 39˚15,8"; 39˚16,3 "; 39˚16,2". Ugyanezt a szöget mértük egy nagy pontosságú goniometrikus eszközzel, amely 39 4216 "42" eredményt eredményezett. Ezt a pontos értéket figyelembe véve számítsa ki a négyzet standard hibáját, határozza meg a UPC megbízhatóságát, keresse meg a marginális hibát.
| Mérési szám | Mérési eredmények, l |
hibák |
∆2 |
| 1 | 39˚17,4 " | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| összeg | 3.42 |
39˚16 "42" = 39˚16,7 "
RMS hiba: m = √ ([∆2 ] / n),
m = √ (3,42 / 8) = 0,65 ".
A UPC megbízhatóságának értékelése: mm = m / √2n,
mm = 0,65 / 16 = 0,1625-0,16 ".
Korlátozási hiba: ∆ stb = 3Hm,
∆pr = 3Ч0,65 "= 1,96"
2. teszt
A háromszögek maradványainak halmaza 50 egységnyi háromszög. Feltételezve, hogy az eltérések valódi hibák, kiszámítjuk az átlagos négyzethibát, és kiszámítjuk a UPC megbízhatóságát, számítsuk ki a marginális hibát. Ezen a készleten ellenőrizze a véletlenszerű hiba tulajdonságait:
Lim [∆] / n = 0, amelyre W = [W] / n számításra kerül.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / nW = +2,51 / 50 = 0,05
A standard hiba ebben az esetben ajánlott a következő képlettel számítani: m = √ (- [W]2 / n) h (n-1),
m = √ (76,5703 - (2,512) / 50) h 49 = 1,249
A UPC megbízhatóságának értékelése a következő képlettel: mm = m / √2 (n-1),
mm = 1,249 / √ (2Ч49) = 0,13.
A hibahatár a következő képlettel: ∆ stb = 3Hm,
Pr = 3,249,2 = 3,747.
5. teszt
Határozza meg a képlettel kiszámított UPC távolságot
S = √(x2 - x1) 2 + (y2 - y1) 2
ha x2 = 6 068 740 m; y2 = 431,295 m;
x1 = 6 068 500 m; y2 = 431,248 m;
mx = my = 0,1 m.
S = √(6 068 740 - 6 068 500)2 + (431 295 - 431 248)2 =235,36
mm = 0,1 / √4 = 0,05
6. cél
Ugyanezt a szöget 5-ször mértük: 60˚41 "; 60˚40"; 60˚40 "; 60˚42"; A mérési eredmények sorozatának matematikai feldolgozása.
| Nn / n | l, ˚ | ε, " | v, " | v2, " |
| 1 | 60˚41 " | 1 | -0,2 | 0,04 |
| 2 | 60˚40 " | 0 | +0,8 | 0,64 |
| 3 | 60˚40 " | 0 | +0,8 | 0,64 |
| 4 | 60˚42 " | 2 | -1,2 | 1,44 |
| 5 | 60˚41 " | 1 | -0,2 | 0,04 |
| összeg | 4 | 0 | 2,8 |
l0 a mért mennyiség minimális értéke, l0 = 60˚40 "; ε a fennmaradó rész ε = l1 - l0; L a mért mennyiség legjobb értéke,
L = [l] / n; m = √ ([v2] / (n - 1), ahol v az aritmetikai átlagtól való eltérés. M az aritmetikai átlagérték pontosságának becslése, M = m / √ n.
L = 60˚40 "+ 4/5 = 60˚40,8"
m = .82,8 / 4 = 0,7 "
M = 0,7 "/ 5 = 0,313"
7. ellenőrzési feladat
Végezze el a mérési eredmények matematikai feldolgozását ugyanazon kontúr területének méretmérőjével: 26,31; 26.28; 26.32; 26.26; 26,31 ha.
| Nn / n | l, ha | ε, ha | v, ha | v2, ha |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| összeg | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18 / 5 = 26,296 ha
m = .000,0029 / 4 = 0,0269 ha
M = 0,0269 / 5 = 0,01204 ha
Ellenőrzési kihívás 8
A kiegyenlítő rúd centiméteres szakaszainak a Genfi vonal segítségével végzett vizsgálatában a hőmérsékletet a jelentés készítésének időpontjában határozták meg. Öt centiméteres szegmensek esetében a következő értékeket kaptuk: 20,3 °; 19,9˚; 20,1˚; 20,2˚; 20,3˚. A mérési eredmények matematikai feldolgozása.
| Nn / n | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5 | 20,3 | 0,4 | 0,14 | 0,0196 |
| összeg | 1,3 | 0 | 0,1128 |
L = 19,9 + 1,3 / 5 = 20,16 °
m = 0,128 / 4 = 0,168
M = 0,168 / 5 = 0,075 °
3.3 Mérési súlyok
Súlymérés - ez egy absztrakt szám, fordítottan arányos a UPC mérési eredmény négyzetével.
Súly formula:
P = K / m2 ,
ahol P a mérési eredmény súlya,
K egy tetszőleges állandó szám egy adott méréssorozathoz,
m - UPC mérési eredmény.
A képletből látható, hogy minél kisebb a UPC mérés, annál pontosabb és nagyobb súlya van.
A két mérés súlyának aránya fordítottan arányos a mérések UPC négyzetével, azaz:
P1 / P2 = m22 / m12
Ha több mérés van l1, l2, ..., ln, akkor nyilvánvaló, hogy egy mérés súlya kisebb lesz, mint az értékek számtani átlagának súlya, azaz:
ahol m az egyik dimenzió hibája,
M az aritmetikai középérték hibája.
Ezután a súlyok aránya fordítottan arányos a UPC négyzeteinek arányával:
PM / Pm = m2 / M2, M = m / √n;
PM / Pm = m2 / (m / √n) 2 = m2 / (m2 / n) = m2Hn / m2 = n.
Így az aritmetikai átlagérték tömege több, mint egy n érték. Következésképpen az aritmetikai középpont súlya megegyezik a méretek számával, amelyből az összeáll.
A nem egyenlő értékű mérések teljes számtani átlaga megegyezik a frakcióval, melynek számlálója a mérési eredmények számtani átlagértékeinek összege súlyukkal, és a nevező a mérések összes súlyának összege. Következésképpen a teljes számtani középpont súlya megegyezik az egyenlőtlen árammérések súlyának összegével:
A0 = (a1P1 + a2P2 + ... + anPn) / (P1 + P2 + ... + Pn),
ahol A0 az általános számtani közep,
ai egyetlen mérés eredménye,
Pi az egyetlen mérés súlya.
Bármely mérési eredmény CSP-je megegyezik a mérési hibával, amelynek súlya 1, osztva az eredmény súlyának négyzetgyökével, azaz:
ahol m a mérési eredmény UPC-je;
M a mérési hiba, amelynek súlya 1;
P a mérési eredmény súlya.
Az 1-es súlyú UPC-mérések megegyeznek a frakció négyzetgyökével, amelynek számlálója az egyenlőtlen dimenziók méréseinek abszolút hibáinak négyzeteinek összege, és a nevezőben az egyenlőtlen dimenziók méréseinek száma.
M = √ (∑∆2P / n),
ahol ∆ a nemlineáris mérés abszolút hibája;
P a súlya;
n a mérések száma.
9. ellenőrzési feladat
A szögmérések eredményei m1 = 0,5; m2 = 0,7; m3 = 1,0. Számítsa ki a mérési eredmények súlyát.
P = K / m2 ;
P1 = 1 / (0,5) 2 = 4;
P1 = 1 / (0,7) 2 = 2,04;
P1 = 1 / (1,0) 2 = 1.
Válasz: 4; 2,04; 1.
11. ellenőrzési feladat
Keresse meg a maradék súlyát a háromszög szögének összegében, ha minden szöget egyenlően mérünk.
m = √ / (n-1), n = 3
m = √ [V21 + V22 + V23] / (3 - 1) = √ [V21 + V22 + V23] / 2
P = K / √ [V21 + V22 + V23] / 2 = 2 K / √ [V21 + V22 + V23] = 2 / ∑ V2i
3.4 A mérési eredményeken alapuló funkciók és azok pontosságának értékelése
A geodéziai munkák során a kívánt értékeket gyakran a számítások eredményeként kapják meg, a mért értékek függvényében. Az így kapott értékek (eredmények) olyan hibákat tartalmaznak, amelyek függnek a függvény típusától és az általuk kiszámított érvek hibájától.
Az azonos értékű ismételt mérésekkel hasonló kapcsolatok sorozatát kapjuk:
Az összes egyenlőség mindkét oldalát négyzetre osztja, és az összeget n:
(∆U12 + ∆U22 +… + ∆Un2) / n = k2Ч (12l12 + ∆l22 + ... + ∆ln2) / n;
∑∆U2 / n = k2Ч (∑∆l2 / n);
m = √ (∑∆U2 / n);
ahol ml - UPC távolságmérés.
Egy állandó értékű termék UPC függvénye egy argumentummal egyenlő az UPC argumentum állandó értékének termékével.
Az U = l1 + l2 űrlap funkciója
Határozzuk meg a UPC-t, ahol az l1 és l2 független withl1 és ∆l2 hibakódok. Ezután az U összeg tartalmazza a hibát:
∆U = ∆l1 + ∆l2.
Ha az addend értékét n-szer méri, akkor elképzelhető:
∆U1 = ∆l1 "+ ∆l2" - 1. dimenzió,
∆U2 = ∆l1 "+ ∆l2" - 2. mérés,
…………………
∆Un = ∆l1 (n) + ∆l2 (n) az n. Dimenzió.
Miután az egyenlőség mindkét oldalát négyszögletesítettük, kifejezést adunk hozzá és n:
∑∆U2 / n = (∑∆l12) / n + 2Ч (∑∆l1Ч∆l2) / n + (∑∆l22) / n.
Mivel a kettős termékben ∆l1 és productl2 különböző jelei vannak, kompenzálni és osztani egy végtelenül nagy n számmal, elhanyagolhatjuk a kettős terméket.
mU2 = ml12 + ml22;
mU = √ (ml12 + ml22).
A két mért érték összegének CSP értéke megegyezik a CSP kifejezés négyzetének összegének négyzetgyökével.
Ha a kifejezések azonos EUC-vel rendelkeznek, akkor:
mU = √ (m2 + m2) = m2m2 = m√2.
Általános esetben:
ahol n az argumentumok száma l.
Az U = l1 - l2 űrlap funkciója
mU = √ (ml12 + ml22).
A két értékmérés közötti különbség UPC-je megegyezik a csökkentett és kivont UPC négyzetek összegének négyzetgyökével.
Az U = l1 - l2 + l3 űrlap funkciója
mU = √ (ml12 + ml22 + ml32 ...)
Az n mért értékek összegének UPC-je megegyezik a UPC négyzetének összes kifejezés négyzetgyökével.
Az U = k1l1 + k2l2 + ... + knln formájának lineáris funkciója
mU = √ [(k1ml1) 2 + (k2ml2) 2 +… + (knmln) 2],
azaz Egy argumentum konstans értékű termékének algebrai összegének UCS-je megegyezik az UPC-nél a konstans értékű termékek négyzetének négyzetgyökével.
Az U = ƒ (l1, l2, ..., ln) általános űrlap funkciója
Ez a matematikai függőség legáltalánosabb esete, beleértve a fenti funkciókat is, amelyek egy speciális eset. Ez azt jelenti, hogy az l1, l2, ..., ln érveket bármely egyenlet adhatja meg. Az ilyen összetett funkció CSP-jének meghatározásához a következőket kell tennie:
1. Keresse meg a funkció teljes különbségét:
dU = (d / dl1) ddl + (d / dl2) dd2 + ... + (d / dln) ddln,
ahol (dƒ / dl1), (dƒ / dl2), ..., (dƒ / dln) a függvény részleges származékai az egyes argumentumokhoz képest.
2. Cserélje ki a különbségeket a megfelelő UPC négyzeteivel, és adja meg a különbség négyzetes együtthatóit:
mU2 = (d / dl1) 2 ml12 + (d / dl2) 2 ml22 + ... + (d / dln) 2 ml.
3. Számítsa ki a részleges származékok értékeit az érvek értékei tekintetében:
(dƒ / dl1), (dƒ / dl2), ..., (d / dln).
Ezután mU = √ [(dƒ / dl1) 2 × ml12 + (dƒ / dl2) 2 × ml22 +… + (dƒ / dln) 2 × mln2].
Az általános űrlap függvényének CSP-je megegyezik a részleges derivatívák termékeinek négyzetgyökének négyzetgyökével, a megfelelő argumentum CSP minden argumentumára vonatkozóan.
3.5 A pontosság becslése a kettős mérések és a tartományok és fordulatok közötti eltérések alapján.
A felmérés gyakorlatában gyakran ugyanazt az értéket mérjük kétszer. Például az útvonali oldalak előre és hátra irányban, a két félfogadó szöge, a magasság - a mérföldkövek fekete és piros oldalán. Minél pontosabbak a mérések, annál jobb az egyes párok eredményeinek konvergenciája.
mlsr. = Ѕ √∑d2 / n
ahol d az egyes párok különbsége; n a különbségek száma.
Bessel-formula:
mlsr = Ѕ √∑d2 / n-1
Ha a méréseknek meg kell felelniük bizonyos geometriai feltételeknek, például a háromszög belső szögeinek összege 180, akkor a mérési pontosságból származó maradékokból a mérések pontossága határozható meg.
μ =√∑ [ f2 / n]/ N,
ahol - egy szögű UPC;
f - maradvány a sokszögben;
N a sokszögek száma;
n a sarkok száma a sokszögben.
4. További tételek meghatározása
4.1 Cél és módszerek további elemek meghatározására
A felvételi hálózattal együtt további pontokat határoznak meg, elsősorban a meglévő geodéziai hálózat filmképzési pontokkal való sűrítésére. Közvetlen, fordított, kombinált és elektronikus távolságmérők jelenlétében - lineáris szerif és ray módszerrel épülnek fel.
Egyes esetekben egy további pontot a koordináták áthelyezése (bontása) határoz meg a jel felső részéről a földre.
4.2 Koordináták átvitele a jel felső részéről a földre. (Példa megoldás)
A topográfiai és geodéziai munkák városi körülmények között történő előállításánál lehetetlen teodolitot létrehozni egy geodéziai hálózat egyik pontján (a lényeg az egyház, az antenna stb.). Ezután feladata, hogy a földön lévő háromszögelési pont koordinátáit lebontják a térségben a geodéziai munkák előállításának biztosítása érdekében.
Alapvonal: A pont az XA, YA koordinátákkal; geodéziai hálózati pontok B (XB, YB) és C (XC, YC).
Terepi mérések: b1 és b "1 bázisok lineáris mérése, I1, I" 1, I2, I "2; b, b vízszintes szögek mérése.
Meg kell találni a P - XP, YP pont koordinátáit.
A probléma megoldása a következő szakaszokra oszlik:
Egy numerikus példa megoldása
Nyers adatok
DAR távolság kiszámítása
Fordított problémamegoldás
Az αAR = αD irányszögek kiszámítása
sin ψ = DЧsinб / S AB; sin = 174,52CH0,66179 / 3068,48 = 0,03950;
sin ψ "= DЧsinб" / S АС; sin `= 174,52CH0,95061 / 5275,51 = 0,03292;
ψ = arcsin 0,03950 = 2 o15`50``;
ψ "= arcsin 0,03292 = 1 o53" 13``;
φ = 180 o - (b + ψ) = 180 o - (138o33` 49`` + 2 o15` 50``) = 39o10` 41``
φ` = 180 o - (b` + ψ`) = 180 o - (71o55` 02`` + 1 o53` 13``) = 106 o11` 46``
αD = αAB ± φ = 329o07` 55`` + 39o10` 41` = 8o18` 36``
αD` = αAC ± φ` = 262o07` 51`` + 106 o11` 46`` = 8o18` 37``
szabályozás:
(aD-a "D) xmp;
ahol mβ a vízszintes szögek FSC mérése.
Az irányszög kiszámításához használt képletekben a "+" vagy "-" jelzés az A, P, B és C pontok relatív helyzetétől függ.
(8o18` 36``-8o18` 37``) ≤ 30``
0o00` 01`` ≤ 30``
Közvetlen problémák megoldása (a koordináták kiszámítása tp)
Xp = XA + AX, Yp = YA + ΔY,
Х "p = ХА + ∆Х", Y "p = YА + ∆Y".
∆X = DcosαD, ∆Y = DsinαD,
∆Х "= Dcosα" D, ∆Y "= Dsinα" D.
A koordináták eltérése nem haladhatja meg a hmYaHp értéket, ahol p = 206265 ", mI - a szögmérés standard hibája.
A P. pont pozíciójának meghatározásának pontosságának értékelése
Az egyetlen tétel meghatározásának standard hibáját a következő képlettel számítják ki:
M2p = m2X + m2Y, M2p = m2D + (D × mα / P) 2
ahol mD - a lineáris mérések pontossága és m α - határozza meg a szögmérések pontosságát.
Például: mD = 2cm, mα = 5``
Mp = √ [(0,02) 2+ (170 × 5/2 × 1010) 2] ≈ 2 × 10–2 = 0,02 m.
4.3 Közvetlen és fordított rezekció megoldása (a feladat változata)
Egy pont koordinátáinak meghatározása szerifivel (Young képletei)
Egyszeri szérum esetén két szilárd ponttal kell rendelkeznie. A meghatározás ellenőrzését a harmadik szilárd ponttól származó másodlagos szerifikus vizsgálattal végezzük.
Alapvonal: szilárd A bekezdés (XAYA); B (XBYB); C (CHC).
Terepi mérések: vízszintes szögek β1, β 2, β`1, β`2.
A P. pontot határozzuk meg.
A probléma megoldására szolgáló képletek:
Xp-XA = ((XB-XA) ctg β 1+ (YB-YA)) / (ctg β 1+ ctg β2);
Xp = XA + ∆XA;
Yp-YA = ((YB-YA) ctg β 1+ (XB-XA)) / (ctg β 1+ ctg β2); Yp = YА + ΔYА;
A P. pont meghatározásának pontosságának értékelése
A UPC számítása az első és a második definícióból:
M1 = (p ^ (S12 + S22)) / pЧsiny1;
M2 = (mp3 (S12 + S22)) / pЧsiny2;
A fenti képletekben szereplő értékek a következők:
mp = 5 ", p = 206265"; y = 73˚15,9 "; y = 62˚55,7 "; S1 = 1686,77 m; S2 = 1639,80 m; S3 = 2096,62 m.
Az oldalsó sorozatokat az inverz problémák megoldása során találjuk.
M1 = (5``, 2,86 + 2,69) / (2-105-0,958) = 0,06 m.
M2 = (5``Ч√, 69 + 4,41) / (2-105-0,890) = 0,07 m.
Mr = √ (M12 + M22); Mr = √ [(0,06) 2+ (0,07) 2] = 0,09 m.
A két definíció koordinátái közötti eltérés
r = √ [(Xp-X`p) 2+ (Yp-Y`p) 2] nem haladhatja meg a 3-as értéket;
r = √ [(2833.82-2833.82) 2+ (2116.38-2116.32) 2] = .000,0036 = 0,06 m.
Az r = 0,06 m 3 × 0,09 m egyenlőtlenség alapján logikus megállapítani, hogy a P. pont definíciója kvalitatív.
A koordináták végső értékei a két definíció átlaga.
Egy numerikus példa megoldása
|
|
(XB-XA) ctg β1 |
|
||||
| XB- XA | YB-YA | |||||
| ctg β1 + ctg β2 4133.41 A tervezési terület fizikai és földrajzi jellemzői. A fő geodéziai keret jellemzői. A kurzus geometriai paraméterei (fordított geodéziai problémák megoldása alapján). A nyúlás kritériumai. Számítási pontosság poligonometrikus pálya. A földgazdálkodási tárgyak felmérése és azoknak a bejelentése, akiknek jogait a végrehajtás során befolyásolhatják. A földgazdálkodás tárgyának határainak meghatározása a földön, azok koordinációja és konszolidációja. Állami, referencia- és felmérési geodéziai hálózat. A fényképezés és a geodéziai keret létrehozásának módszerei. A légi felvételek tervezett-magassági előkészítése és értelmezése. Terv kidolgozása a munka hatékonyságának javítására. A terepi célok meghatározása. Az objektumon végzett munka mennyiségének kiszámítása. A geodéziai rajzok fő típusai. A terv és a térképek megkülönböztető jelei. A teodolit alapellenőrzése és beállítása. A geodéziai tanulmány lényege. Geodéziai támogatás az oszlopok üvegalapú telepítéséhez. Az oszlopok függőleges igazítása. Topográfiai felmérési módszerek. Teodolit T-30 és vele együtt dolgozni. Teodolit szintezés. Mensal lövés. Felületi szintezés. Tacheometriai felmérés. Mérnöki problémák megoldása a tervben. A topográfiai felmérési módszerek összehasonlító elemzése. Ez a kiadvány összefoglalja a műholdas geodéziai módszerek használatának tapasztalatait a bányászati vállalkozásokban zajló geodinamikai folyamatok megfigyelésére. A trigonometrikus szintezés különböző módszereinek elmélete. A trigonometrikus szintezés hibái a mért távolságok pontosságától függően. Geodéziai módszerek az állami geodéziai hálózat pontjainak középpontjainak meghatározására. Az előzetes számítások célja a poligonometriában. Munka koordináták kiszámítása. Szögletes és lineáris mennyiségek kiegyenlítése. A csomópontpont koordinátáinak korrigált értékeinek súlyozása. A terepi mérések pontosságának becslése és egy csomópont koordinátáinak kiszámítása. Elektronikus állomások: típusok, működési elv, főbb előnyök, alkalmazások és szabványos alkalmazási feladatok. Az elektronikus állomás ellenőrzése. A tacheométer előkészítése a tachometriai felméréshez és a mérések eredményeinek feldolgozásához. Olyan technika, amely lehetővé teszi egy ismétlődő algoritmus használatát a súlyos hibák és a geodéziai hálózatok későbbi kiegyenlítésének ellenőrzésére a mérnöki struktúrák és a földfelszín deformációinak megfigyelése során. A program blokkja a tervezett deformációk elemzésére. A föld (szekció, szétválás, társulás, újraelosztás) és a tulajdonhoz való jog állami szabályozásának megvizsgálása. A kataszteri nyilvántartás alapjainak megismerése. A tervezett geodéziai hálózat létrehozásának folyamatának leírása. A sűrítőhálózatokban a geodéziai mérések eredményeinek matematikai feldolgozásának módja. A további pontok koordinátáinak kiszámítása közvetlen és inverz többszörös sarokszegmensekkel. A poligonometria rendszer kiegyenlítése. A geodéziai eszközök ismerete. A teodolit 4Т30 tervezési jellemzői, a 3Н-5Л szint és az elektronikus 3/3 állomás. Geometriai, trigonometrikus, hidrosztatikus, barometrikus szintezés. Automatizálás tacheometriai felmérése. A geodéziai hálózatok rögzítésének jelei, azok érték szerinti besorolása, elhelyezkedése, kijelölése a területen. Lakó-, lakossági, ipari épületek. A geodéziai munkák előállításának szakaszai az objektum építése során. A háromszögelés, a tervezett felmérési hálózat elmozdulásának rendszerei, a teodolit egy csomóponttal mozog, és a teodolit és a poligonometriai mozdulatok szögei egymást követő közelítésekkel. A referencia vonalak irányszögeinek kiszámítására szolgáló séma. |
3.2 A geodéziai mérések hibáinak osztályozása. RMS hiba. Gauss és Bessel formái a számításhoz
A nagyon jó körülmények között elvégzett geodéziai mérések hibákat is okoznak, azaz az L mérési eredmény eltérése a számozott mennyiség X-es értékétől:
Az igaz egy olyan mérhető mennyiség értéke, amely ideálisan tükrözné egy objektum mennyiségi tulajdonságait. Az elérhetetlen feltétel - valódi érték - hipotetikus fogalom. Ez egy olyan érték, amely végtelenül közelíthető meg, nem érhető el.
Mérési pontosság - az eredmény közelítésének mértéke a valós értékhez. Minél alacsonyabb a hiba, annál nagyobb a pontosság.
Az abszolút hibát a mérés eredményeként kapott érték és a nagyságmérés valós értékének különbsége adja. Például, ha a tényleges érték l = 100 m, ugyanazon vonal mérésekor az eredmény 100,05 m, akkor az abszolút hiba:
E = X ism - X
E = 100,05 - 100 = 0,05 (m)
Az érték megszerzéséhez elég egy mérés elvégzése. Ezt szükségesnek nevezik, de gyakrabban nem korlátozódik egy dimenzióra, hanem legalább két alkalommal megismétlik. Azokat a méréseket, amelyek túlmutatnak a szükségeseken, redundánsnak (kiegészítőnek) nevezzük, ezek a mérés eredményének nagyon fontos eszközei.
Az abszolút hiba nem ad képet az eredmény pontosságáról. Például 0,06 m-es hiba lehet az l = 100 m vagy l = 1000 m mérésével, ezért a relatív hibát kiszámítjuk:
C = 0,06 / 100 = 1/1667, azaz 1667 m-en mért 1 méteres hiba történt.
Relatív hiba - az abszolút hiba és a tényleges vagy mért érték aránya. Express frakció. Az utasítások szerint a terepvonalat nem szabad durvábbra mérni, mint 1/1000.
Az egyes tényezőkből eredő hibákat elemi névnek nevezik. Az általánosított hiba az elemi összeg összege.
Vannak:
· Durva (Q),
· Rendszeres (O),
· Véletlen (∆).
A hibás, a vállalkozó hibái, a gondatlansága, a technikai eszközök észrevétlen hibái miatt durva mérési hibák keletkeznek. A durva hibák teljesen elfogadhatatlanok, és ismételt, további mérésekkel teljesen ki kell zárni a mérési eredményekből.
Szisztematikus mérési hibák - a hibával kapcsolatos állandó összetevő: látás, műszaki eszközök meghibásodása, hőmérséklet. A szisztematikus hibák egyoldalúak és változóak lehetnek (időszakos hibák). Amikor csak lehetséges, munkájuk megszervezése és lebonyolítása során azokat a mérési eredményeket figyelembe veszik vagy kizárják.
A véletlen mérési hibák elkerülhetetlenül kísérik az összes mérést. A véletlenszerű hibák nem zárhatók ki, de a kívánt eredményre gyakorolt hatásuk további mérésekkel csökkenthető. Ezek az összes méréssel kapcsolatos legrosszabb hibák. Lehet, hogy a méret és a jelzés is különbözik.
Ha bruttó és szisztematikus hibákat lehet vizsgálni és kizárni a mérési eredményből, akkor a véletlenszerű hibákat mély mérés alapján lehet figyelembe venni. A valószínűségi elméleten alapuló tanulmány.
A gyakorlatban a nehézség abban rejlik, hogy a méréseket korlátozott számú alkalommal hajtjuk végre, és ezért a mérések pontosságának becsléséhez a szórás becsült becslését, amit RMS-hibának nevezünk.
A Gauss-t az átlag négyzetes hibára vonatkozó képlet javasolta:
∆ 2 cf = (∆ 2 1 + ∆ 2 2 + ... + ∆ 2 n) / n,
∆ 2 = m 2 = (∆ 2 1 + ∆ 2 2 +… + ∆ 2 n) / n,
∆ cf = m = √ (∑ ∆ 2 i / n)
A képletet akkor alkalmazzák, ha a hibákat a valós értékekből számítják ki.
Bessel-formula:
m = √ (∑V 2 i / (n-1))
Az aritmetikai átlag rms-hibája Önnél kisebb, mint az egyéni mérés rms-hibája.
Becslésekor a pontossági mértékegységként az egynél nagyobb súlyú standard hibát alkalmazzák. A súlyegység átlagos négyzetes hibája.
µ 2 = P × m 2 - µ = m √ P, m = µ / √ P, azaz a mérési eredmények átlagos négyzetes hibája megegyezik a mérési hibával, amelynek súlya 1 (µ), és osztva az eredmény (P) súlyának négyzetgyökével.
Kellően nagy számú méréshez írhatunk ∑m 2 P = ∑∆ 2 P ((= m) óta:
µ = √ (∑ (∆ 2 × P) / n), azaz az 1-es egyenlő súlyú átlag négyzetmérési hiba megegyezik a számláló négyzetgyökével, amelynek súlya az egyenlőtlen dimenziós mérések abszolút hibahelyeinek termékeinek összege, és a nevezőben az egyenlőtlen dimenziós mérések száma.
A teljes aritmetikai átlag átlagos négyzetes hibája a következő képlettel:
M 0 = µ / √∑P
Az µ értékét helyettesítő µ:
M 0 = √ (∑∆ 2 × P / n) / (√∑P) = √ [(∑∆ 2 × P) / n × (∑P)]
M 0 = √ [(Δ 1 2 P 1 + Δ 2 2 P 2 +… + Δ n 2 P n) / n × (P 1 + P 2 +… + P n)] a Gauss képlet, a teljes kvadratikus hiba a teljes az aritmetikai középpont egyenlő a frakció négyzetgyökével, amelynek számlálója az egyenlőtlen árammérések hibáinak négyzeteinek összege a súlyukhoz, és a nevező a súlyuk összegeinek számának eredménye.
µ = √ [∑ (V 2 × P) / (n-1)] Ez a Bessel-képlet az aritmetikai átlaghiba kiszámításához 1-es súlyméréssel a nem egyenlő hosszúságú mérések sorozatánál a valószínű hibák alapján. Nagyszámú mérésre érvényes, és korlátozott (gyakran a gyakorlatban) hibákat tartalmaz: m µ = µ / a µ becslés megbízhatósága.
Teszt probléma 1
A teodolit tanulmányozására többször ugyanazt a szöget méri. Az eredmények a következők: 39˚17,4 "; 39˚16,8"; 39˚16,6 "; 39˚16,2"; 39˚15,5 "; 39˚15,8"; 39˚16,3 "; 39˚16,2". Ugyanezt a szöget mértük egy nagy pontosságú goniometrikus eszközzel, amely 39 4216 "42" eredményt eredményezett. Ezt a pontos értéket figyelembe véve számítsa ki a négyzet standard hibáját, határozza meg a UPC megbízhatóságát, keresse meg a marginális hibát.
| Mérési szám | Mérési eredmények, l | hibák | ∆2 |
| 1 | 39˚17,4 " | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| összeg | 3.42 |
39˚16 "42" = 39˚16,7 "
RMS hiba: m = √ ([∆ 2] / n),
m = √ (3,42 / 8) = 0,65 ".
A UPC megbízhatóságának értékelése: m m = m / √2n,
m = 0,65 / 16 = 0,1625-0,16 ".
Limit hiba: ∆ pr = 3 × m,
∆ pr = 3 × 0,65 "= 1,96"
2. teszt
A háromszögek maradványainak halmaza 50 egységnyi háromszög. Feltételezve, hogy az eltérések valódi hibák, kiszámítjuk az átlagos négyzethibát, és kiszámítjuk a UPC megbízhatóságát, számítsuk ki a marginális hibát. Ezen a készleten ellenőrizze a véletlenszerű hiba tulajdonságait:
Lim [∆] / n = 0, amelyre W = [W] / n számításra kerül.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n, W = + 2,51 / 50 = 0,05
A standard hiba ebben az esetben célszerű kiszámítani a következő képlettel: m = √ (- [W] 2 / n) ÷ (n-1),
m = √ (76,5703 - (2,51 2) / 50) ÷ 49 = 1,249
A UPC megbízhatóságának értékelése a következő képlettel: m m = m / √2 (n-1),
m m = 1,249 / √ (2 × 49) = 0,13.
Korlátozási hiba a következő képlet szerint: Δ pr = 3 × m,
∆ pr = 3 × 1,249 = 3,747.
5. ellenőrzési feladat Határozza meg a képlettel kiszámított UPC távolságot
S = √ (x 2 - x 1) 2 + (y 2 - y 1) 2
ha x 2 = 6 068 740 m; y2 = 431,295 m;
x 1 = 6 068 500 m; y2 = 431 248 m;
m x = m y = 0,1 m.
S = √ (6 068 740 - 6 068 500) 2 + (431 295 - 431 248) 2 = 235,36
m m = 0,1 / 4 = 0,05
6. cél
Ugyanezt a szöget 5-ször mértük: 60˚41 "; 60˚40"; 60˚40 "; 60˚42"; A mérési eredmények sorozatának matematikai feldolgozása.
| Nn / n | l, ˚ | ε, " | v, " | v2, " |
| 1 | 60˚41 " | 1 | -0,2 | 0,04 |
| 2 | 60˚40 " | 0 | +0,8 | 0,64 |
| 3 | 60˚40 " | 0 | +0,8 | 0,64 |
| 4 | 60˚42 " | 2 | -1,2 | 1,44 |
| 5 | 60˚41 " | 1 | -0,2 | 0,04 |
| összeg | 4 | 0 | 2,8 |
l 0 a mért mennyiség minimális értéke, l 0 = 60˚40 "; ε a fennmaradó rész ε = l 1 - 0; L a mért mennyiség legjobb értéke,
L = [l] / n; m = √ ([v 2] / (n - 1), ahol v az aritmetikai átlagtól való eltérés. M az aritmetikai átlagérték pontosságának becslése, M = m / √ n.
L = 60˚40 "+ 4/5 = 60˚40,8"
m = .82,8 / 4 = 0,7 "
M = 0,7 "/ 5 = 0,313"
7. ellenőrzési feladat
Végezze el a mérési eredmények matematikai feldolgozását ugyanazon kontúr területének méretmérőjével: 26,31; 26.28; 26.32; 26.26; 26,31 ha.
| Nn / n | l, ha | ε, ha | v, ha | v2, ha |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| összeg | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18 / 5 = 26,296 ha
m = .000,0029 / 4 = 0,0269 ha
M = 0,0269 / 5 = 0,01204 ha
Ellenőrzési kihívás 8
A kiegyenlítő rúd centiméteres szakaszainak a Genfi vonal segítségével végzett vizsgálatában a hőmérsékletet a jelentés készítésének időpontjában határozták meg. Öt centiméteres szegmensek esetében a következő értékeket kaptuk: 20,3 °; 19,9˚; 20,1˚; 20,2˚; 20,3˚. A mérési eredmények matematikai feldolgozása.
| Nn / n | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
Nem szükségesek, akkor az eszközt manuálisan kell kifejleszteni, ha azt az eltöltött idő és az anyagi erőforrások szempontjából indokolták. 2. Geodéziai mérések feldolgozása táblázatok segítségével A topográfiai és geodéziai munkák komplexumából nyert információk kezdeti feldolgozásához a TOGI programot használtam, amely egy csomag ...
Az építkezésen meg kell felelni az SNiP Sh-4-80 "Biztonság az építésben" fejezetben és a tanszék utasításaiban leírt biztonsági előírásoknak és szabályoknak. Azok a személyek, akiket az építési menedzsment megbízásából utasítottak, geodéziai munkákat végezhetnek. A sérülés vagy sérülés kockázata a munkavállaló körülményeitől függően határozható meg.
Elektronikus eszközök a szerző közvetlen részvételével. Második fejezet A második fejezetben a metrológiai berendezések és a geodéziai mérőeszközök ellenőrzésére és kalibrálására szolgáló padok kutatására vonatkozó kidolgozott módszerek kerülnek áttekintésre. A geodéziai műszerek függőleges szögeinek mérésére szolgáló rövid időtartamú hiba vizsgálatának módszere. Fontos feladat a tanulmányban ... |
A MÉRÉSI EREDMÉNYEK FELDOLGOZÁSA
A fizikai gyakorlatban
Mérések és mérési hibák
A fizika kísérleti tudomány, ami azt jelenti, hogy a fizikai törvényeket a kísérleti adatok összegyűjtésével és összehasonlításával állapítják meg és ellenőrzik. A fizikai műhely célja, hogy megtanulják a tapasztalatokból a fő fizikai jelenségeket, megtanulják, hogyan kell helyesen mérni a fizikai mennyiségek számértékeit, és összehasonlítani azokat az elméleti képletekkel.
Minden mérés két típusra osztható - egyenes vonalakés közvetett.
a közvetlen A kívánt értéket közvetlenül a mérőberendezés leolvasásából nyerjük. Például a hossza egy vonalzóval, az órával eltelt idővel stb.
Ha a kívánt fizikai mennyiséget nem lehet közvetlenül mérni az eszköz által, és a képlet segítségével mért értékek segítségével fejezzük ki, akkor az ilyen méréseket nevezzük közvetett.
Bármely érték mérése nem ad abszolút pontos értéket ennek az értéknek. Minden mérés mindig hibát tartalmaz (hiba). A hiba a mért és a valós érték közötti különbség.
A hibák általában osztva vannak szisztematikus és véletlen.
szisztematikusan hívja a hibát, amely állandó marad a mérések sorozatában. Az ilyen hibák a mérőműszer tökéletlensége (például az eszköz nulla eltolása) vagy a mérési módszer miatt következnek be, és elvileg kizárhatók a végeredményből a megfelelő korrekció bevezetésével.
A szisztematikus hibák magukban foglalják a mérőeszközök hibáját is. Bármely műszer pontossága korlátozott, és pontossági osztálya jellemzi, amely általában a mérési skálán látható.
véletlen hiba történt, amely különböző kísérletekben változik, és lehet pozitív és negatív is. A véletlenszerű hibák a mérőeszköztől (súrlódás, rések, stb.) És külső körülmények (rezgés, hálózati feszültségingadozások stb.) Függő okai miatt következnek be.
A véletlen hibákat nem lehet empirikusan megszüntetni, de az eredményre gyakorolt hatásuk ismételt mérésekkel csökkenthető.
ÁLTALÁNOS ÉRTÉK ÉS ÁLTALÁNOS TULAJDONSÁGI HIBA.
Tegyük fel, hogy egy sor mérést végzünk az X nagyságrendben. A véletlenszerű hibák miatt n különböző értékek:
X 1, X 2, X 3 ... X n
Egy átlagos értéket általában mérési eredményként veszik figyelembe.
Az átlag és az eredmény közötti különbség i -a mérés mértékét a mérés abszolút hibájának nevezzük.
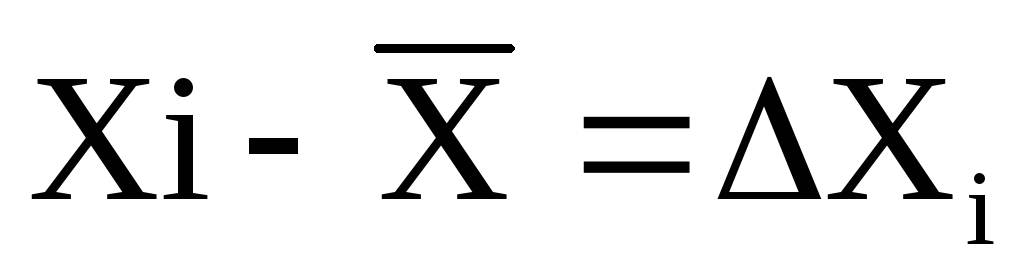
Az átlag hiba hibájának mérésére az egyéni mérés abszolút hibájának átlagértéke lehetséges.
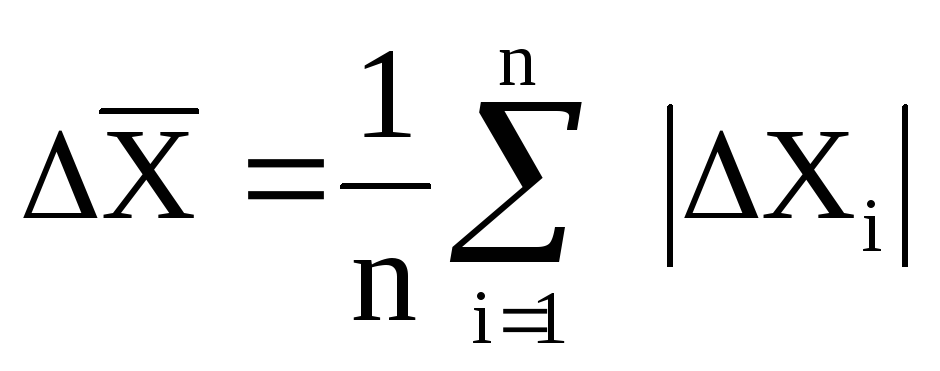(2)
érték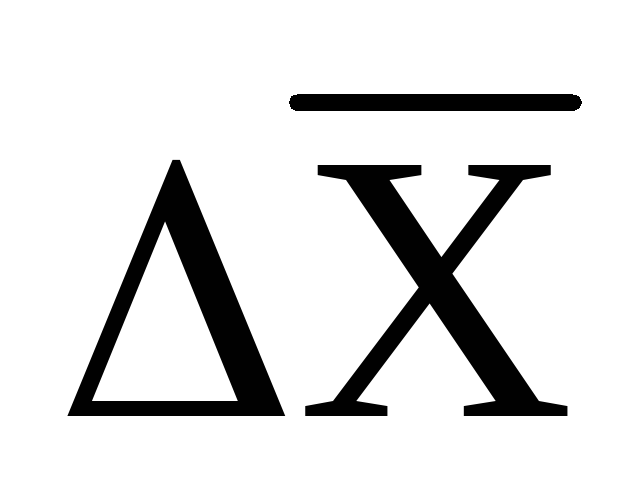 
az aritmetikai átlag (vagy abszolút abszolút) hibája.
Ezután a mérési eredményt úgy kell írni, mint a
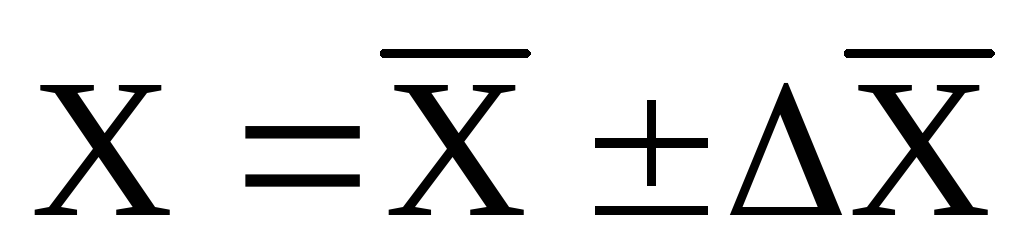(3)
A mérések pontosságának jellemzése a relatív hiba, amelyet általában százalékban fejezünk ki
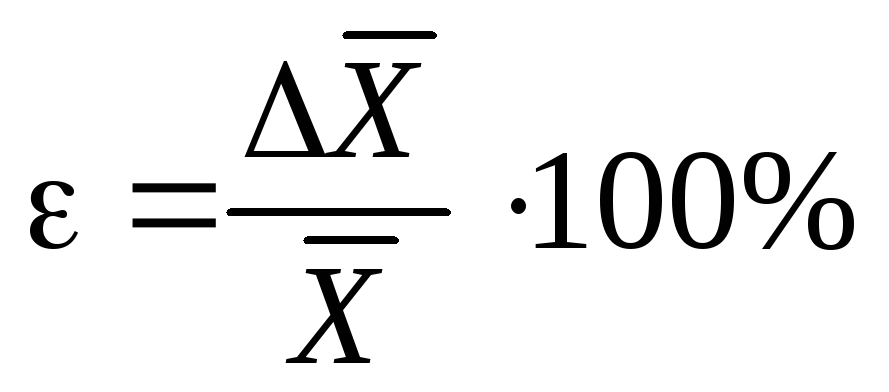(4)
KÖZVETLEN SQUARE ERROR.
Kritikus méréseknél, amikor szükséges a kapott eredmények megbízhatósága, a standard error (vagy szórás) értéket kell használni, amelyet a képlet határoz meg.
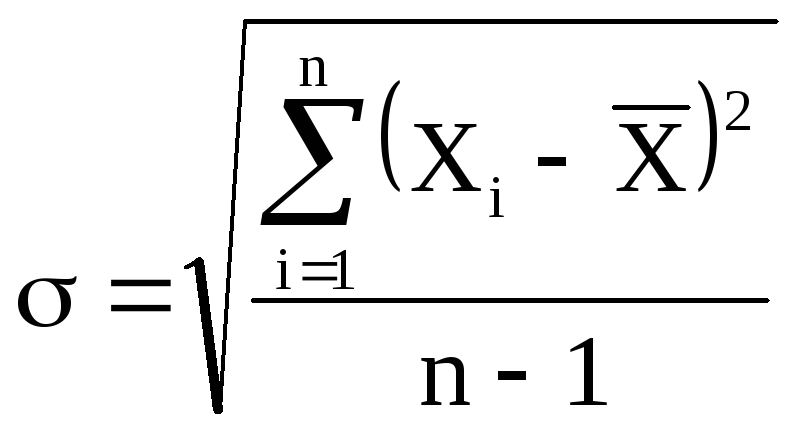(5)
Az érték az egyetlen egység eltérését mutatja a valódi értéktől.
Ha számítunk n mérések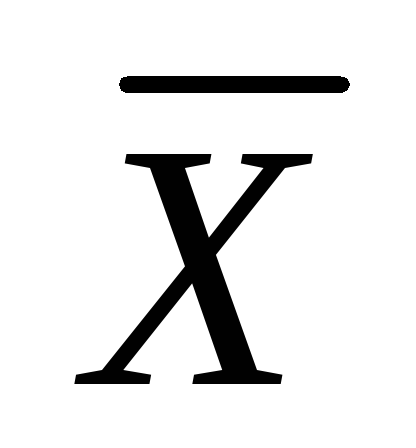 
a (2) képlet szerint ez az érték pontosabb lesz, vagyis kevésbé fog különbözni az igazitól, mint minden egyes dimenzió. Az átlag négyzethibája 
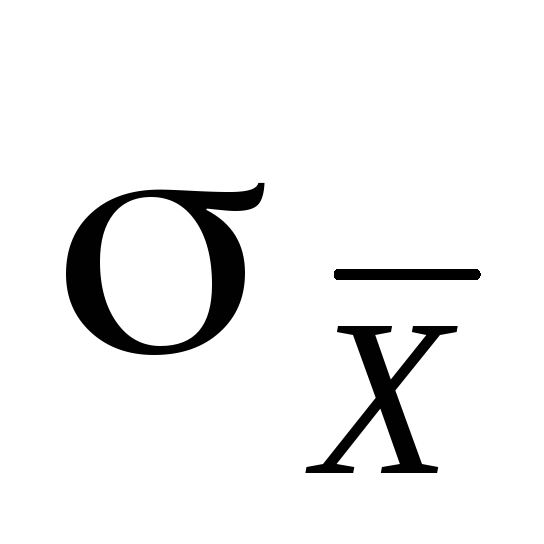jelentése
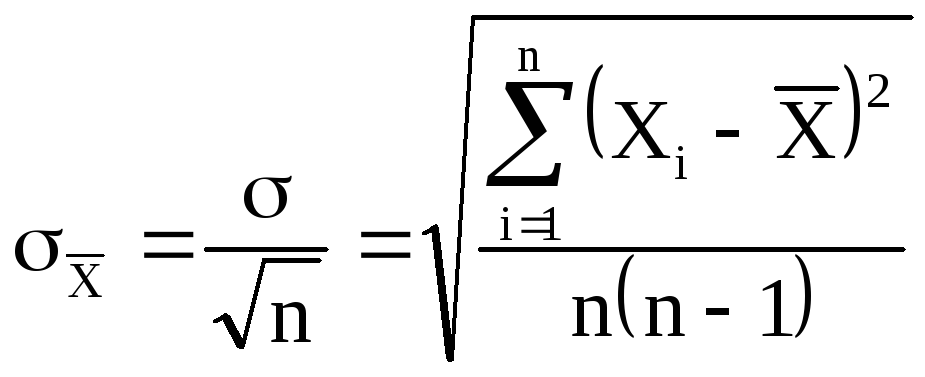(6)
ahol az egyes mérések rms hibája, n - a mérések száma.
Így a kísérletek számának növelésével csökkenthető az átlagos érték véletlenszerű hibája.
Jelenleg a tudományos és technikai mérések eredményeit általában az űrlapon mutatják be
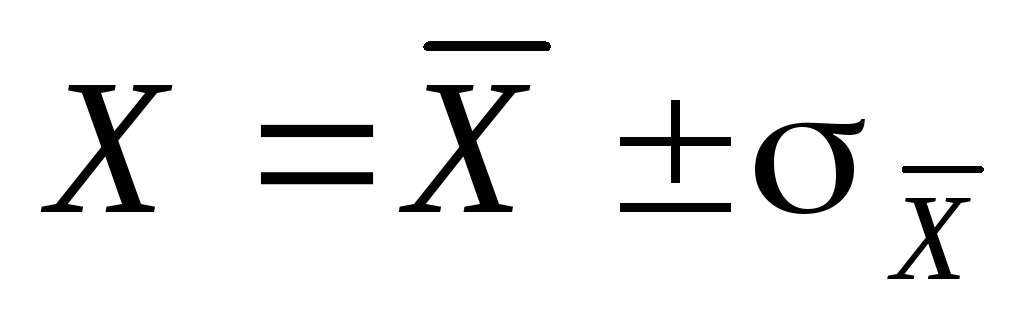(7)
Ahogy az elmélet azt mutatja, egy ilyen rekordgal tudjuk, hogy a kapott eredmény megbízhatósága, vagyis az igazi érték X68% valószínűleg más 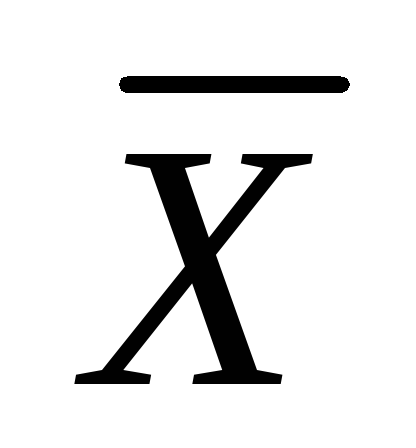nem több, mint .
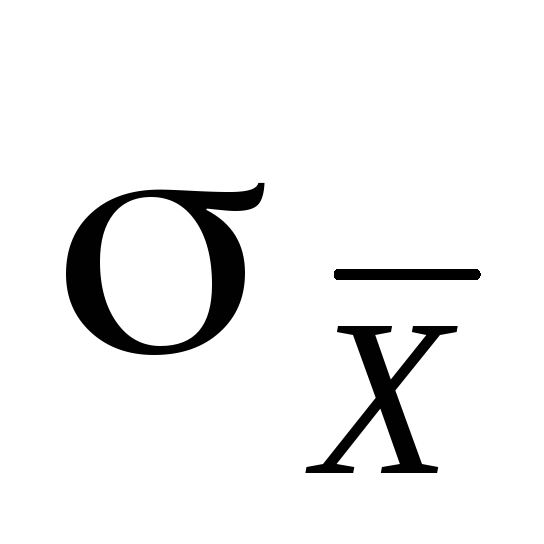Ha az aritmetikai átlag (abszolút) hibát használja (2. képlet), semmi nem mondható el az eredmény megbízhatóságáról. Ebben az esetben a mérések pontosságának bizonyos elképzelései viszonylagos hibát adnak (4. képlet).
A laboratóriumi munka során a diákok mind az átlagos abszolút hibát, mind az átlag négyzethibát használhatják. A pályázók közül melyiket kell közvetlenül megadni minden egyes munkában (vagy a tanár által jelzett).
Általában, ha a mérések száma nem haladja meg a 3 - 5 értéket, akkor egy átlagos abszolút hiba használható. Ha a mérések száma körülbelül 10 vagy annál nagyobb, akkor az átlag négyzethibájánál helyesebb becslést kell alkalmazni (5. és 6. képlet).
A SYSTEMATIC ERRORS KONTOZÁSA.
A mérések számának növelésével csak véletlen tapasztalati hibák csökkenthetők, de nem szisztematikusak.
A rendszeres hiba maximális értékét általában az eszközön vagy az útlevélben jelzik. A hagyományos fém vonalzóval végzett méréseknél a szisztematikus hiba legalább 0,5 mm; féknyereg mérésére -
0,1 - 0,05 mm; mikrométer - 0,01 mm.
Gyakran a műszer divízió árának felét szisztematikus hibának tekintik.
Az elektromos mérőműszerek mérlegei jelzik a pontossági osztályt. A K pontossági osztály ismeretében lehetőség van a készülék ∆Х szisztematikus hibájának kiszámítására a képlettel
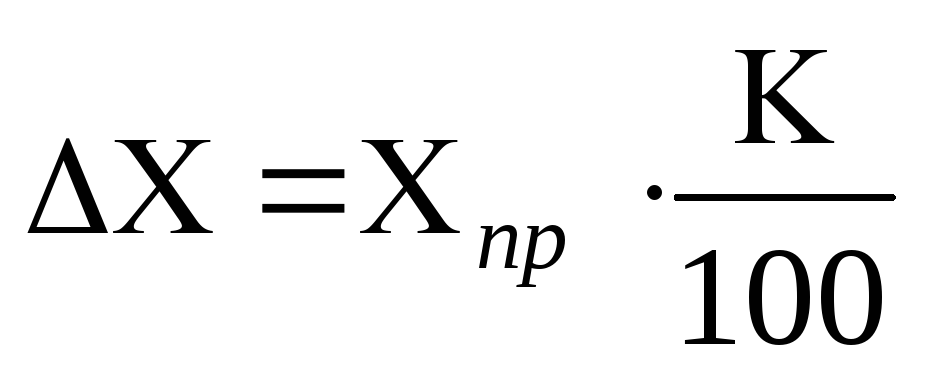
ahol K a műszer pontossági osztálya, X pr a mérőeszköz skáláján mérhető határérték.
Tehát az 5A-ig terjedő skálán lévő 0,5-ös osztályú ampermérő az áramot legfeljebb 1-es hibával méri
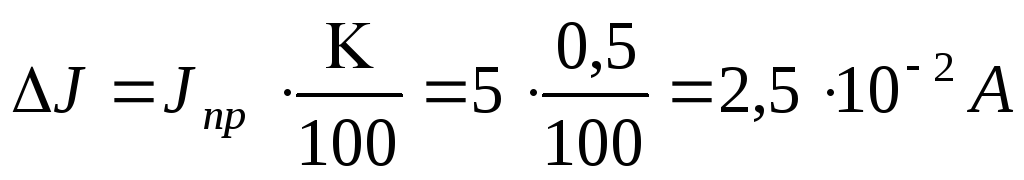
A digitális eszköz hibája megegyezik a legkisebb kijelző számmal.
A teljes hiba átlagos értéke: véletlenés szisztematikusanhibákat.
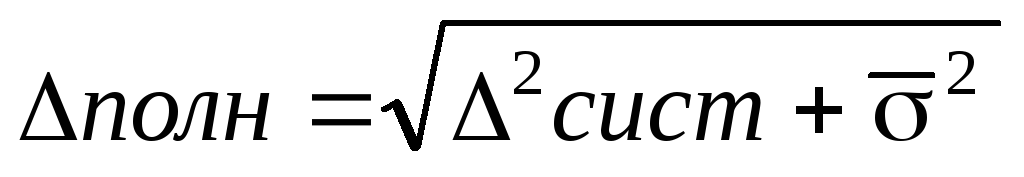
A válasz szisztematikus és véletlenszerű hibákkal kerül rögzítésre az űrlapon
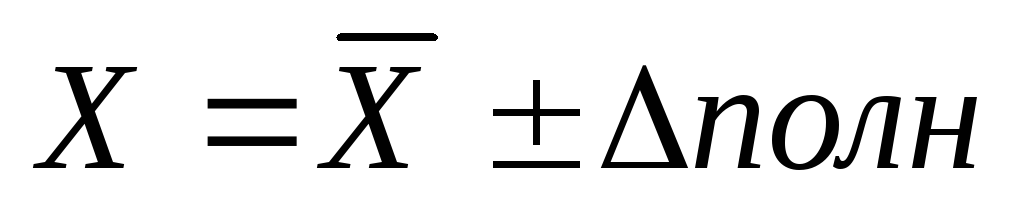
KÜLÖNLEGES MÉRÉSEK HIBÁK
A fizikai kísérletekben gyakran előfordul, hogy maga a kívánt fizikai mennyiség nem mérhető tapasztalattal, hanem a közvetlenül mért más mennyiségek függvénye. Például egy henger térfogatának meghatározásához meg kell mérni a D átmérőt és a magasságot hmajd számítsuk ki a térfogatot a képlettel
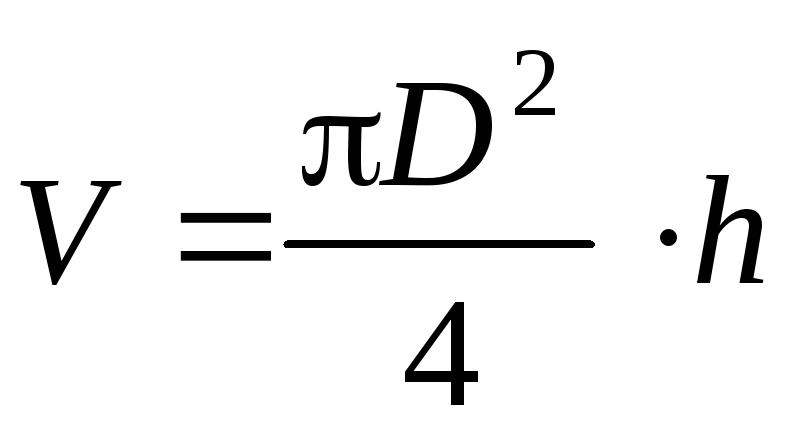
érték Dés hvalamilyen hibával mérjük, következésképpen a számított értéket V ez némi hibával is kiderül. A mért értékek hibáin keresztül képesnek kell lennie kifejezni a számított érték hibáját.
A közvetlen mérésekhez hasonlóan lehetséges az átlagos abszolút (aritmetikai átlag) hiba vagy az átlagos négyzethiba kiszámítása.
A hibák mindkét esetben történő kiszámításának általános szabályait differenciális számítással nyerjük.
Legyen a φ kívánt érték több változó függvénye X, Y,Z…
φ( X, Y,Z…).
Közvetlen mérésekkel megtalálhatjuk az értékeket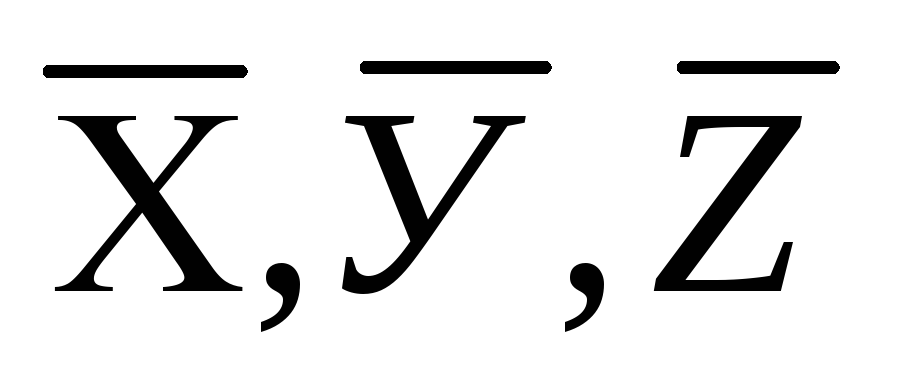 
és értékelje az átlagos abszolút hibákat 
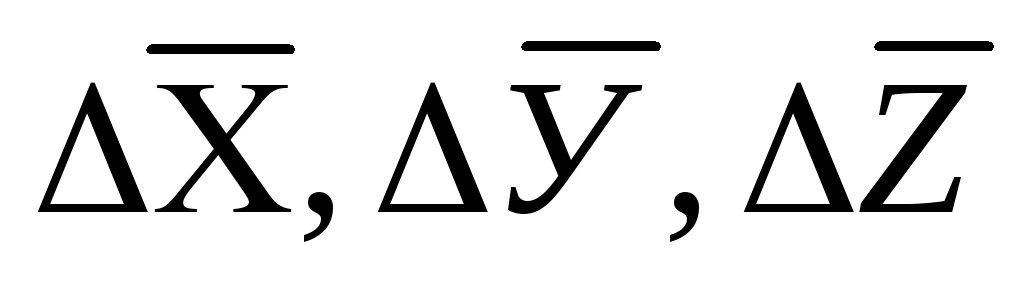... vagy átlagos négyzethibák X, Y, Z ...
Ezután az aritmetikai átlagos hibát a képlettel számítjuk ki
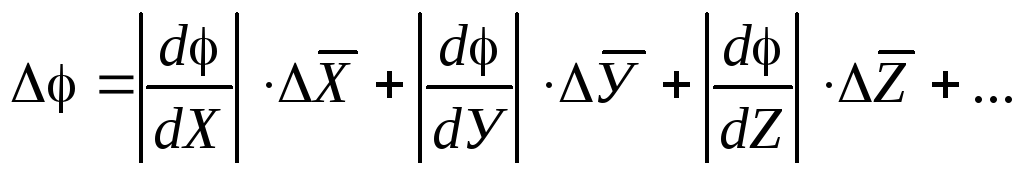
ahol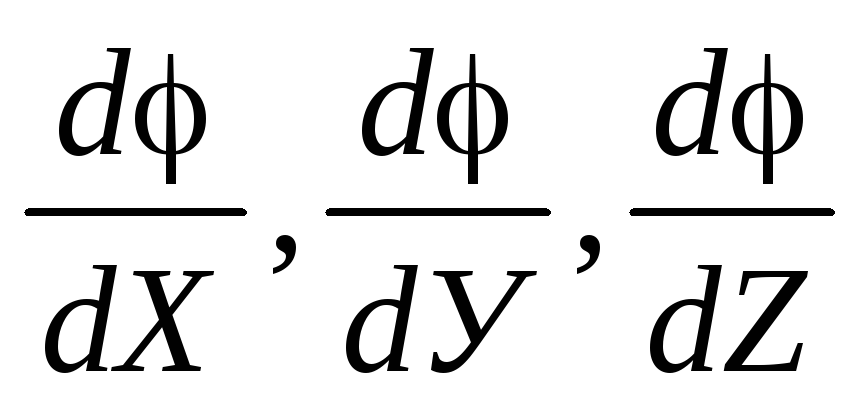 
- φ részleges származékai X, Y,Z.
Ezeket az átlagértékekre számítják …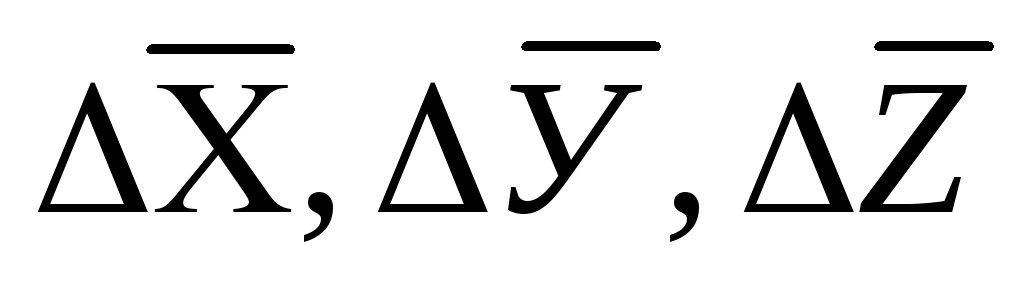
Az átlagos négyzethibát a képlettel számítjuk ki
Példa erre.A hengermennyiség kiszámításához a hibakezeléseket kapjuk.
a) A számtani átlag hiba.
érték D és h ennek megfelelően egy error hibával mérhető D és h.
b) Az átlagos négyzethiba.
érték D és h measured D, h hibával mérve .
A kötet hibája egyenlő lesz
Ha a képlet egy logaritmizálásra alkalmas kifejezést jelent (azaz egy terméket, frakciót, fokozatot), akkor a relatív hibát először kiszámítani kell. Ehhez (a számtani átlag hiba esetén) a következőket kell tenni.
1. Prologizálja a kifejezést.
2. Különbözze el.
3. Kombinálja az összes kifejezést ugyanazzal a különbséggel, és tegye ki a zárójelből.
4. Vegyük a kifejezést a különböző modulok modulok előtt.
5. Cserélje ki a differenciális jelvényeket d abszolút hiba ikonokon.
Az eredmény a relatív hiba képlete
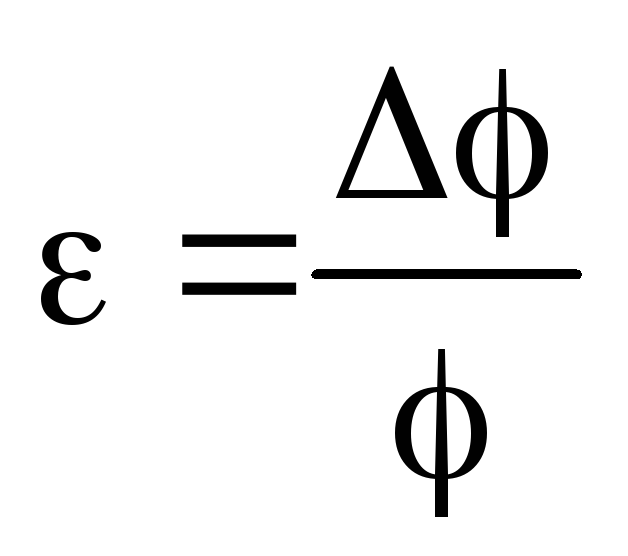
Aztán owing ismeretében kiszámíthatja az abszolút hibát
=
Példa erre.
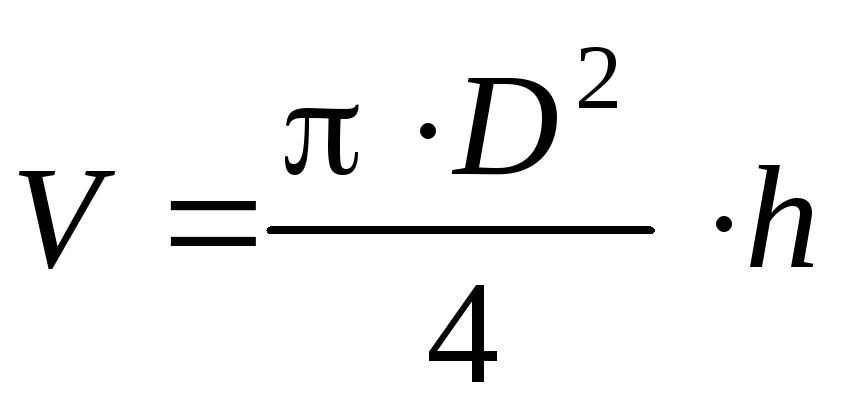
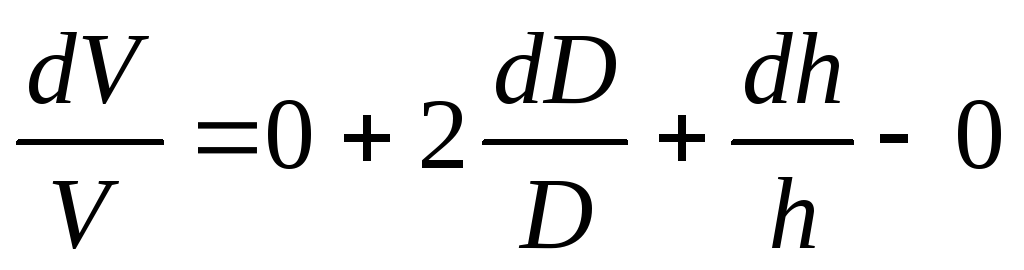
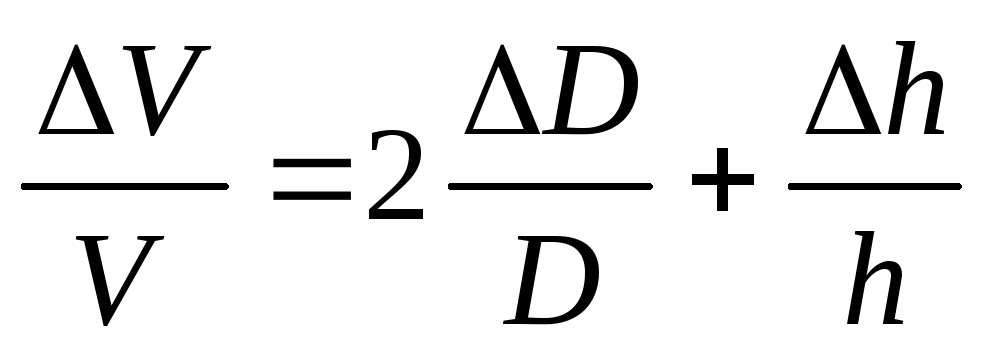
Hasonlóképpen, meg tudjuk írni a relatív átlagos négyzethibát
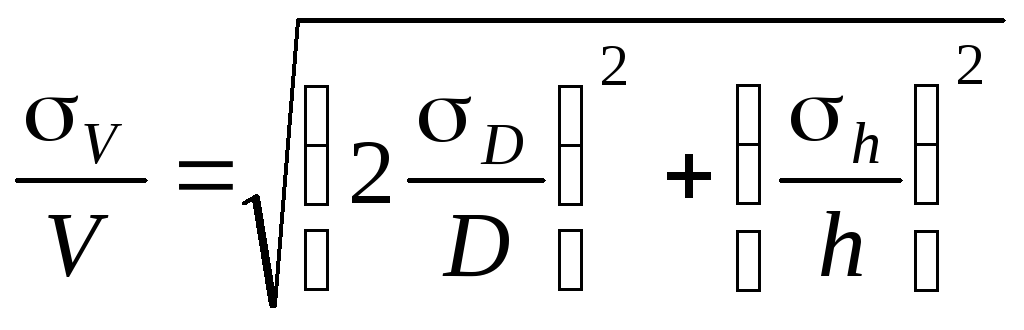
A mérési eredmények bemutatásának szabályai a következők:
a hibát egy jelentős számjegyre kell kerekíteni:
helyesen = 0,04,
rossz - = 0,0382;
az eredmény utolsó jelentős számjegyének ugyanolyan nagyságrendűnek kell lennie, mint a hiba:
helyesen = 9.830.03,
rossz - = 9,8260,03;
ha az eredmény nagyon nagy vagy nagyon kicsi, akkor a rekord indikatív formáját kell használni - ugyanaz az eredmény és annak hibája, és a tizedespontnak az eredmény első számjegyét kell követnie:
helyesen - = (5.270.03) 10 -5,
rossz - = 0,00005270.0000003,
= 5,2710 -5 .000,0000003,
= = 0,0000527310 -7,
= (5273) 10 -7,
= (0,5270,003) 10 -4.
Ha az eredmény egy dimenzióval rendelkezik, meg kell adnia azt:
helyesen - g = (9.820.02) m / s 2,
helytelen - g = (9.820.02).
Rajzolási szabályok
1. A grafikonok grafikonra épülnek.
2. A rajzolás előtt egyértelműen meg kell határozni, hogy melyik változó egy argumentum, és melyik függvény. Az argumentumértékeket az x tengelyen ábrázolják (a x), a függvényértékek az y tengelyen (tengely a).
3. A kísérleti adatokból az érvelés és a függvény változásának korlátai.
4. Jelölje meg a koordináta tengelyeken elhelyezett fizikai mennyiségeket, és jelölje meg a mennyiségegységeket.
5. Helyezze fel a diagramot a kísérleti pontokra, jelezve őket (kereszt, kör, félkövér).
6. Rajzoljon egy sima görbét (egyenes vonalat) a kísérleti pontokon úgy, hogy ezek a pontok a görbe mindkét oldalán megközelítőleg azonos számban találhatók.
A hibák típusai. RMS hiba. - Oktatási rész, A navigációban használt koordinátarendszerek: gömb alakú, poláris, ortodromikus. Majdnem mindig hiba történt ...
A hibák típusai.Szinte mindig a hiba két részből áll: szisztematikus és véletlenszerű.
Δa = Δa sist + Δ a eset.
szisztematikusanaz úgynevezett hiba, amely ezekben a körülmények között állandó értéket (vagy változásokat, de ismert törvény szerint) megtart.
Ezeket a hibákat a folyamatos működés okai okozzák, aminek következtében a mérés során minden alkalommal ugyanazzal az összeggel hibázunk. Nagyon gyakran az ilyen hibákat a műszer hibás gyártása okozza (instrumentális hibák), vagy állandó külső tényező. Például a repülőgép saját mágneses mezője hibát okoz a mágneses pálya (eltérés) mérésekor, amely minden egyes pályán határozott értékkel rendelkezik.
A rendszeres hibák, mivel minden mérésnél azonosak, pontosabb eszközök segítségével egyszer meghatározhatók, majd korrekciók megadásával kizárhatók a mérési eredményekből.
A szisztematikus hibák nem okoznak nagy bajt a navigálás során, mivel megszűnésük után már hiányoznak. Ezért azt is feltételezzük, hogy nincsenek szisztematikus hibák (amelyeket már figyelembe vettek).
Véletlen hibaminden mérés más értéket vesz fel, és nem ismert előre, melyik.
A véletlenszerű hibák azonban elvben nem szüntethetők meg, mivel az egyes méréseknél eltérőek. És mindig ismeretlenek maradnak.
Nem lehet meghatározni a véletlenszerű hibák számszerű értékeit, de a pilótának folyamatosan szem előtt kell tartania, hogy ezek a hibák léteznek, és megértik a lehetséges értékeket. A mérési eredmények bizonytalansága az egyik fő tényező, amely bonyolítja a navigációt, és nem csak a tudomány és a művészet.
A véletlen esemény olyan esemény, amely az adott körülmények között előfordulhat vagy nem fordulhat elő. Egy ilyen esemény lehetőségének számát a valószínűség nagysága jellemzi. A P valószínűsége 0-tól 1-ig terjedő szám. Ha az ilyen körülmények között soha nem fordul elő esemény, akkor lehetetlen eseménynek hívják, és annak valószínűsége nulla. Ha ez mindig az adott körülmények között történik, akkor azt hitelesnek nevezik, és egy valószínűséggel egyenlő. Ha például P = 0,3, akkor ez azt jelenti, hogy 100 esetben 100 esetben átlagosan az esemény bekövetkezik. Átlagosan, mert az esemény véletlen. Ha létrehoz egy olyan eseményt, amely egy esemény előfordulásához szükséges, és 100 kísérletsorozatot végez, akkor egy esemény előfordulhat, például 23-szor, vagy 32-szer. Minél nagyobb a végzett kísérletek száma, annál közelebb kerül az esemény átlagos előfordulási száma a kísérletek teljes számának 30% -ára (ha P = 0,3).
Hogyan lehet leírni a véletlenszerű hibákat, ha nincs különösebb jelentése? Gyakran jellemzik az átlag négyzethibát (CSP), amelyet az σ (sigma) betű jelez. Például az a mennyiségű UPC méréseket σa jelöli.
Az UPC a mért érték diszperziós fokának a jellemzője annak tényleges értékénél. Minél nagyobb az σa, annál szétszórtabb (szóródott) a különböző kísérletekben mért értékek a mennyiség tényleges értéke körül.
Az 1. ábrán A 2,19 geometriai ábrázolás a számított tengely lehetséges értékei egyés megjegyezte annak tényleges értékét. A skála keresztjei a több kísérlet eredményeként kapott mért értékeket jelzik. Az első esetben a tényleges érték körüli mért értékek szóródása nagyobb, mint a második esetben, ezért a „sigma”, amely a szórás mértékét jellemzi, a második esetben kisebb.
Ábra. 2.19. RMS hiba
Az EUC értékének megfelelően megítélhető, hogy a mért érték egy vagy másik értéket vesz fel. Ehhez azonban nem elég tudni az EUC-t, tudnod kell, hogy milyen disztribúciós jogot alkalmaz a véletlen hiba. Sok véletlen változó betartja a normál (Gauss) elosztási törvényt. Ehhez a törvényhez hasznos a következő értékek emlékeztetése.
Ha nincs szisztematikus hiba, és a mérés eredményeképpen az aizmus értékét kapjuk, akkor a mennyiség tényleges értéke belül van (2.20. Ábra):
aizmus ± σa valószínűséggel = = 0,68;
aizmus ± 2σa valószínűséggel = = 0,95;
az aizmus ± 3σa a valószínűséggel P = 0,997.
Ábra. 2.20. Néhány valószínűség a normál eloszláshoz
Például egy iránytű használatával mérjük a γ = 100º pályát, és az iránytű pontosságát az σγ = 2º EUC jellemzi. Ez azt jelenti, hogy a tényleges árfolyam (amely számunkra ismeretlen marad) átlagosan:
68 esetben a 100-ból 100 ° ± 2 ° -on belül van, azaz a 98 ° ... 102 ° -on belül;
a 100-ból 100 esetben 100 ° ± 4 ° -on belül van, azaz a 96 °… 104º-os tartományban van;
997 esetben az 1000-ből 100 ° ± 6 ° -on belül van, azaz a 94 °… 106º-os tartományban van.
Valószínűségi érték P= 0,997 olyan közel van ahhoz, hogy a "három sigma" megfelelő hibája gyakran a legnagyobb hiba. Valójában a hiba meghaladhatja azt. Igaz, ritkán - átlagosan három esetben az ezerből.
A műszerek és berendezések műszaki leírásában pontosságukat közvetlenül a UPC formában lehet feltüntetni, majd minden világos. Néha azonban ez a következő: „csapágymérési hiba ± 1,5º”. Természetesen ez nem jelenti azt, hogy egy ilyen irányjelző minden alkalommal 1,5 ° -kal „téved”. Ez nem jelenti azt, hogy nem tévedhet. többmint 1,5º. Általában a hiba meghatározott értéke megfelel a valószínűségnek P= 0,95. Ez átlagosan a 100-ból 95 esetben van, a hiba nem haladja meg (felfelé vagy lefelé) az 1,5º-os értékeket.
Ennek megfelelően a száz esetből öt esetben a hiba több lehet. A normál hibaelosztási jog esetében a 0,95 valószínűsége megfelel kétszerUPC. Ezért a csapágy UCS mérése ebben a példában 0,75º lesz.
A munka vége -
Ez a téma a következőhöz tartozik:
Polar koordinátarendszer ... Távolság a koordinátarendszer eredetétől az objektumpontig ...
Ha ehhez a témához további anyagra van szüksége, vagy nem találta, amit keresett, javasoljuk, hogy használja az adatbázisunkban található keresést:
Ha ez az anyag hasznosnak bizonyult az Ön számára, mentheti azt a szociális hálózatokon lévő oldalára:
| csipog |
A navigációban használt koordinátarendszerek (gömb alakú, poláris, ortodromikus).
Ha a navigációs problémák megoldásának nagyon nagy pontossága nem szükséges, akkor a Föld gömbnek tekinthető. Ebben az esetben a normál gömb koordinátarendszert használjuk, amelynek pólusai
Navigációs és repülési elemek.
Aerobatikus elemek. A navigáció és a kísérletezés légiforgalmi irányítási folyamatok. Ennek a mozgásnak a leírásához navigációs és aerobatikus értékeket használnak.
Szél és jellemzői. Ekvivalens szél.
A légköri légtömegek szinte mindig mozgásban vannak, amit a földfelszín különböző területein a hőmérséklet és a nyomás különbsége okoz. Az ilyen mozgalom okai és jellege tanulmányozásra kerül
Navigációs háromszög sebesség. A szélsebesség és a szögszög függése a szélszögben.
A nap a levegő tömegéhez viszonyítva a tényleges V sebességgel, a levegő tömegével a földhöz viszonyítva U sebességgel és a nap mozgási sebességével viszonyítva.
A tanfolyammérés elvei és a tanfolyamok típusai.
A pálya a repülőgép hossztengelyének irányát vízszintes síkban jellemzi, azaz azt mutatja, hogy a repülőgép „orrát” irányítják. Fontos a navigáció szempontjából, mert egyszerre
Eltérés, típusai, elszámolása repülés közben.
Nyilvánvaló, hogy ugyanazon a ponton a két mágneses mező nem létezhet egyszerre, két intenzitásvektor - a Föld (H) és a sík (F). ezek
A mágneses iránytű használatára vonatkozó gyakorlati ajánlások.
1. Emlékeztetni kell arra, hogy a poláris régiókban, ahol a mágneses dőlés nagy, és ezért a Föld mágneses mezőjének vízszintes összetevője kicsi, a mágneses kompaszok instabilak és
Giroszkópos pálya mérési elv. A giroszkóp kiállítási tengelye, a vízszintes és azimutális korrekció.
A giroszkóp (az ókori görögtől a „forgatásig” és a „megjelenésig”) alapvetően bármilyen forgó test. A modern technológiában a giroszkóp meglehetősen nagy forgórész nagy sebességgel.
Gyropolukompas GPK-52. A gyropolucompass ortodromicitása.
Gyropolukompas GPK-52. A giroszkópos pályaeszközök működésének elve az egyik ilyen legegyszerűbb eszköz - a giroszkóp félvezető GPC-52 - példája.
Orthodromy tanfolyam gyro
Most, miután elemeztük a címsor győri magatartását egy álló síkon, megvizsgáljuk, hogyan fog viselkedni, amikor a repülőgép ortodrom vonal mentén mozog. Általános eset - n
Referencia meridián és ortodrom tanfolyam. Konverziós arányok.
A giroszkóp tengelye a repülés kezdetén bármilyen irányba beállítható. A pilóták arra a tényre használják, hogy a 0 ° -os pálya északra, 90 ° -kal keletre, stb. Ezért a gir számértékei
Alapvető információk a kurzusrendszerekről. Mágneses korrekciós mód.
A két mérési elvnek - a mágneses és a giroszkópiai - mindegyiknek megvan a maga előnye és hátránya. A mágneses iránytűnek az az előnye, hogy lehetővé teszi
Mágneses korrekciós mód
Mint már említettük, a „GPC” módban az árfolyamrendszer hasonló a hagyományos gyropolucompasshoz, ezért ez az üzemmód nem igényel további külön vizsgálatot. Fontolja meg a munkát
A rádiómagasságmérők fogalma
A rádiómagasságmérő (PB) egy autonóm rádiós eszköz. Ez azt jelenti, hogy működéséhez rádióhullámokat használnak, és a földön nincs szükség felszerelésre. december
A működési elv, az eszköz és a hiba barometrikus magasságmérője.
Eszközének elve szerint a barometrikus magasságmérő lényegében egy aneroid barométer, azzal a különbséggel, hogy a skála nem fokozatosan nyomás alatt van, hanem az egységnyi egységben.
Barometrikus magasságmérő hibák
A barometrikus magasságmérőnek számos hibája van, amelyek okaiban különböznek. A különböző tényezők által okozott hibák összeadódnak, hogy egy közös hibát képezzenek - a különbség
Barometriai nullapontszintek
A pilóta elvileg a barometrikus magasságmérő skálára gyakorolt nyomás beállításával választhatja ki azt a szintet, amelytől a magasságot kívánja számolni. De a repülésbiztonság szempontjából
A barometrikus magasságmérő skálán a nyomás beállítására vonatkozó szabályok
Tekintsük a nyomást a SPT-nél a repülés közbeni telepítés sorrendjét. Az országunkban elfogadott hagyományos technológia azt írja elő, hogy az indulást megelőzően minden legénység a magasságmérőjükön
Egy nyíl sebességjelzők
A Bernoulli egyenlet tartalmazza a levegő sűrűségét ρ a patak mindkét szakaszában. Alacsony fordulatszámon (max. 400-450 km / h) és repülési magasságokon (akár 4000-5000 m) a levegő összeegyeztethetetlennek tekinthető
Kombinált sebességjelzők
Nagy sebességeknél és magasságoknál a valós és a műszer sebessége közötti különbség már jelentős. Emellett a levegő összenyomhatósága jelentős hatást gyakorol a nagy sebességekre és magasságokra. A költő
Sebességmérő hibák
Instrumentális hibák ΔV és az eszköz kialakításának tökéletlensége és a kiigazítás pontatlansága miatt keletkeznek. Minden eszköz saját műszeres értékekkel rendelkezik.
A számozás fogalma
Bármely repülés végrehajtásakor a hajózószemélyzet tagjainak bármikor ismerniük kell a légi jármű aktuális helyét. A légi jármű helyének meghatározása - a léginavigáció egyik fő feladata. A léginavigációban
Grafikus számítás
Teljes tömítés. A teljes szalag célja, hogy meghatározza az aktuális MS-t, és ezért természetesen a repülés során végezzük el. Nem gondolja, hogy minden pilóta vagy navigátor elvégezte a repülést
A privát ortodrom koordináták automatikus számításának elve.
A számozás az aktuális koordináták kiszámítása, ezért az automatizált számrendszerek fő része a navigációs számológép. Ez lehet analóg, azaz az alap
Diss. Kursodoplerovskoe és procursus calculus.
A Doppler-sebesség és a drift-mérő (DISS) egy fedélzeti rádióeszköz, amely lehetővé teszi, hogy mérje a föld sebességét és a repülési szögét a repülőgép fedélzetén. DISS a használat alapján
A légi navigáció alapvető szabályai. Ellenőrzési útvonal és típusai.
A repülés során a legénységnek be kell tartania a légi navigáció alapvető szabályait. 1) Az adott repülési pálya fenntartásának ellenőrzése a biztosításához szükséges időközönként
Vizuális orientáció.
A vizuális orientáció az MC meghatározására szolgáló módszer a térkép összehasonlítása és a repült terep alapján. A vizuális tájolás érdekében tájékozódásokat használnak. Navigációs iránypont
A pozíciós vonalak általánosított módszere. Navigációs paraméter, felületi és helyzetvonal.
Navigációs paraméter. A repülőgép elhelyezkedését különböző műszaki eszközökkel, többek között rádiós navigációs segédeszközökkel és különböző módszerekkel lehet meghatározni. De ahogy V.V.
Felület- és helyzetvonal.
Ha a tér bizonyos pontján a navigációs paraméternek határozott értéke van, akkor ez egyáltalán nem jelenti azt, hogy más pontokban értékei szükségszerűen eltérőek lehetnek. az biztos
A pozíciós vonalak típusai.
A navigáció során leggyakrabban navigációs paramétereket használnak, amelyek geometriai értékek, azaz távolságok, szögek stb. Ebben az esetben a navigációs paraméterek minden típusa megfelel
A rádió iránytű rendszer navigációs jellemzői.
A rádióirányító rendszer magában foglalja a földi rádióállomást és a fedélzeti irányjelzőt, az úgynevezett automatikus rádiókompassot (ARC). Mivel a rádióállomások speciálisan telepíthetők
Az ARC elve és beállításainak sorrendje.
A rádió iránytű működési elve a rádióhullámok irányított vételén alapul. Az ARC a következő fő összetevőket tartalmazza: - forgatható hurokantenna; - nem irányított (shly
A PHT repülési módszerei (passzív, természetesen aktív).
A rádióállomásra vagy a rádióállomásról történő repülés módjai. Amint azt korábban jeleztük, a CSD nem navigációs paraméter, mivel ugyanabban a pontban a térben bármilyen érték lehet
Az útvonal irányítása az ARC használatával az RNT-be és az RNT-be történő repülés közben.
Állapotvezérlő út az irányban. Van egy általános „radionavigációs pont” (RNT), amely bármely földfelszíni rádiónavigációs eszköz megjelölésére használható: OP
A vezérlési útvonal tartománya az ARC segítségével.
A pálya távolságvezérlése a megtett távolság meghatározása vagy az MRP-re való fennmaradó távolság meghatározása. Ennek végrehajtásához az ARC és a PRSD is használható. Ehhez természetesen nem lehet a PRSD
Az IPA és az MS meghatározása két rádióállomáson.
Néhány navigációs probléma megoldásához, például az MS meghatározásához, meg kell határozni az LRPS térképet. Ehhez először meg kell határozni a repülőgép csapágyát. Mivel minden térképen alkalmazott
A repülőgép elhelyezkedésének meghatározása két rádióállomáson
A légi jármű helyzetének meghatározása az útvonal teljes ellenőrzése, mert ha ismert a légi jármű ülése, akkor az LZP-től való eltérést (az útvonal irányítását) lehet meghatározni, és a megtett vagy megmaradt távolságot.
Az útvonal korrekciója a kijárattal az MRP-re és a kilépési szög.
Az útvonal javítása az MRP kiadásával. Az útvonal korrekciója az, hogy a repülőgépet egy adott pályára juttassuk, miután észleltünk egy eltérést. Egyféleképpen
Javítási útvonal kilépési szöggel
Korábban az 1. fejezetben megvitatták az útvonal egyik korrekcióját - az MRP kiadásával. Az ilyen módszer azonban a polgári légi közlekedésben elsősorban kis lineáris eltérésekre alkalmazható, például
Mutatók, mint az RMI és az UGR. Repülés az LZP használatával.
A leggyakoribb úgynevezett rádió-mágneses mutatók (RMI). Angolul ugyanúgy hívják őket, mint a rádió mágneses jelző (RMI). A hazai navigációs rendszerek bizonyos típusai
Repülés a rádióállomások igazításakor
Ha a repülést az LZP-n végzik, amelyen két rádióállomás van telepítve, akkor a rádióállomások összehangolásában egy repülésről beszélnek. Ha a nap az RNT (az egyik elöl és a másik mögött) között repül, akkor a célt hívják
Az RNS minimális és maximális hatása.
A minimális cselekvési tartomány. A függőleges síkban a legtöbb földi rádiós navigációs segédeszköz (rádióállomások, rádiójelzők) irányíthatósága körülbelül
Az irányjelző rendszer navigációs jellemzői.
A rádióirányítási rendszer jellemzői. A rádióirányítási rendszer elsősorban a légiforgalmi irányítás (ATC) eszköze. Segítségével a helyszíni légiforgalmi irányító
VOR rádiójeladó rendszer és annak alkalmazása LZP-re történő repülésre, MS meghatározása.
A VOR elve. A rádiójeladó goniometrikus VOR rendszer (nagyon nagy frekvenciájú tartományok) magában foglalja a földi berendezéseket - a VOR rádiójelzőt és a fedélzeti berendezést.
A légi jármű egy rádióállomás helyének meghatározása
A pozíciósorok általánosított módszerével összhangban az MS meghatározásához két navigációs paraméter és két megfelelő pozícióvonal szükséges. Úgy tűnik, hogy ha a rádióállomás csak egy
A távolságmérő rendszerek működésének elve. Döntött és vízszintes tartomány.
DME jellemző. A távolságmérő radionavigációs rendszere (DRNS) magában foglalja a földi berendezéseket (távolságmérő rádiójelző) és a fedélzeti berendezéseket (repülőgép-távolságmérő).
Goniometrikus távolságmérő rendszerek. Navigációs jellemzők RSBN.
A goniometriás rádiós navigációs rendszerek (UDRNS) olyan rendszereket hívnak, amelyek lehetővé teszik, hogy egyszerre két navigációs paramétert mérjenek - a csapágy és a tartomány. Az UDRNS segítségével
A földi radar navigációs jellemzői és azok használata az útvonal nyomon követésére és javítására.
A radar fogalma. A radar alatt (a "rádió" és a hely (lat.) - a hely meghatározásához) a szó szélesebb értelemben értendő, hogy hogyan kell meghatározni a helyet és a karaktert
A zónás navigáció fogalma.
Navigációs útmutatás. Lehetetlen megérteni, hogy mi a zonális navigáció, és a modern navigáció általában, ha nincs olyan fogalma, mint egy navigációs navigáció.
A fedélzeti radar működésének elve. Ellenőrzi a radar "Thunderstorm" -t.
A légi radarállomás (RLS) egy autonóm rádió-technikai eszköz, amely lehetővé teszi a repülőterület radarképének és a környező levegő helyzetének megfigyelését, \\ t
Módszerek az MS meghatározására radar segítségével (goniométer, távolságmérő, goniometriás távolságmérő).
A radar segítségével meghatározhatja, hogy az MS sokkal pontosabb, mint az áttekintő összehasonlító módszer. Ehhez a lokátor képernyőn meg kell mérni a pálya szöget és a referenciaponthoz való távolságot. Tanfolyam sarok ori
Áttekintés és összehasonlító módszer a orientációra a radaron és a meghatározáson, a segítségnyújtás sebességével és a sodrási szöggel.
Tekintettel arra, hogy a repülőterület képe a radar képernyőjén képződik, a pilóta irányíthatja a tájékozódást, ha összehasonlítja a radarképet a repülési térképpel, mint pl.
A talajsebesség és a sodrási szög meghatározása radar segítségével
A talajsebesség meghatározása. Az összes tájékozódási pont a képernyőn, amikor a nap mozog, a nap irányával ellentétes irányban mozog, azaz a képernyőn lefelé. Ima
Az inerciális számítás alapelve
Az inerciális navigációs rendszerek (INS) a repülőgép gyorsulásainak mérésén alapulnak a koordinátarendszer tengelye mentén. A gyorsulásokat a gyorsulásmérőknek nevezett eszközökkel mérik. A működés elve
Az insz. Segítségével meghatározott paraméterek. Szabad formanyomtatványok
Az INS által meghatározott paraméterek Az inerciális rendszerek a repülőgép koordinátáinak meghatározására szolgálnak. De a meghatározásuk során sok d
Ingyenes inerciális navigációs rendszerek
Évtizedek óta a hagyományos ANN-eket fejlesztő mérnökök erőfeszítései arra irányultak, hogy csökkentse a gyroplatformot előre meghatározott helyzetben tartó giroszkópok öngondoskodását. nem
Az ismert szél sebességének és sebességének kiszámítása.
Vizsgáljuk meg a probléma megoldására szolgáló eljárást egy példában a következő kezdeti adatokkal: V = 400; ZMPU = 232; 8 = 290; U = 70; S = 164; ΔM = –4.
A szél meghatározása a repülés során.
Adott: V = 680; W = 590; MK = 312; MS = + 8; ΔM = –4. Keresés: δн, δ, U.
Az igazi sebesség kiszámítása széles nyílban.
A KUS széles nyíl jelzése szerint a valós sebességet a következő képlettel számítjuk ki: Vi = Vpr + ΔV és + ΔVa + ΔV cf + ΔV
