Уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают из года в год в список заданий типа B и C на едином государственном экзамене ЕГЭ. Однако среди большого числа уравнений с параметрами есть те, которые с легкостью могут быть решены графическим способом. Рассмотрим этот метод на примере решения нескольких задач.
Найти сумму целых значений числа a, при которых уравнение |x 2 – 2x – 3| = a имеет четыре корня.
Решение.
Чтобы ответить на вопрос задачи, построим на одной координатной плоскости графики функций
y = |x 2 – 2x – 3| и y = a.
График первой функции y = |x 2 – 2x – 3| будет получен из графика параболы y = x 2 – 2x – 3 путем симметричного отображения относительно оси абсцисс той части графика, которая находится ниже оси Ox. Часть графика, находящаяся выше оси абсцисс, останется без изменений.
Проделаем это поэтапно. Графиком функции y = x 2 – 2x – 3 является парабола, ветви которой направлены вверх. Чтобы построить ее график, найдем координаты вершины. Это можно сделать по формуле x 0 = -b/2a. Таким образом, x 0 = 2/2 = 1. Чтобы найти координату вершины параболы по оси ординат, подставим полученное значение для x 0 в уравнение рассматриваемой функции. Получим, что y 0 = 1 – 2 – 3 = -4. Значит, вершина параболы имеет координаты (1; -4).
Далее нужно найти точки пересечения ветвей параболы с осями координат. В точках пересечения ветвей параболы с осью абсцисс значение функции равно нулю. Поэтому решим квадратное уравнение x 2 – 2x – 3 = 0. Его корни и будут искомыми точками. По теореме Виета имеем x 1 = -1, x 2 = 3.
В точках пересечения ветвей параболы с осью ординат значение аргумента равно нулю. Таким образом, точка y = -3 есть точка пересечения ветвей параболы с осью y. Полученный график изображен на рисунке 1.
Чтобы получить график функции y = |x 2 – 2x – 3|, отобразим симметрично относительно оси x часть графика, находящуюся ниже оси абсцисс. Полученный график изображен на рисунке 2.
График функции y = a – это прямая, параллельная оси абсцисс. Он изображен на рисунке 3. С помощью рисунка и находим, что графики имеют четыре общие точки (а уравнение – четыре корня), если a принадлежит интервалу (0; 4).
Целые значения числа a из полученного интервала: 1; 2; 3. Чтобы ответить на вопрос задачи, найдем сумму этих чисел: 1 + 2 + 3 = 6.
Ответ: 6.
Найти среднее арифметическое целых значений числа a, при которых уравнение |x 2 – 4|x| – 1| = a имеет шесть корней.
Начнем с построения графика функции y = |x 2 – 4|x| – 1|. Для этого воспользуемся равенством a 2 = |a| 2 и выделим полный квадрат в подмодульном выражении, написанном в правой части функции:
x 2 – 4|x| – 1 = |x| 2 – 4|x| - 1 = (|x| 2 – 4|x| + 4) – 1 – 4 = (|x |– 2) 2 – 5.
Тогда исходная функция будет иметь вид y = |(|x| – 2) 2 – 5|.
Для построения графика этой функции строим последовательно графики функций:
1) y = (x – 2) 2 – 5 – парабола с вершиной в точке с координатами (2; -5); (Рис. 1).
2) y = (|x| – 2) 2 – 5 – часть построенной в пункте 1 параболы, которая находится справа от оси ординат, симметрично отображается слева от оси Oy; (Рис. 2).
3) y = |(|x| – 2) 2 – 5| – часть построенного в пункте 2 графика, которая находится ниже оси x, отображается симметрично относительно оси абсцисс наверх. (Рис. 3).
Рассмотрим получившиеся рисунки:
 Графиком функции y = a является прямая, параллельная оси абсцисс.
Графиком функции y = a является прямая, параллельная оси абсцисс.
С помощью рисунка делаем вывод, что графики функций имеют шесть общих точек (уравнение имеет шесть корней), если a принадлежит интервалу (1; 5).
Это можно видеть на следующем рисунке:

Найдем среднее арифметическое целых значений параметра a:
(2 + 3 + 4)/3 = 3.
Ответ: 3.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
ДАГЕСТАНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
ПЕДАГОГИЧЕСКИХ КАДРОВ
КАФЕДРА ФИЗИКО- МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ И ИКТ
Проект
на тему:
« Построение и п реобразования
графиков функций
в школьном курсе математики »
Рабаданова П.А.
учитель математики
МБОУ « Кочубейская СОШ»
Тарумовский район
2015 г.
1. Введение……………………………………………………………….….3
2. Глава I . Обзор литературы по теме проекта………………………….….5
3. Глава II . Эмпирическая часть:
3.1. Основные методы преобразования графиков функции……….….7
3.2. Построение графиков четной и нечетной функций…………….. 10
3.3. Построение графика обратной функции………………………... 11
3.4. Деформация (сжатие и растяжение) графиков ………………….12
3.5.Комбинация переноса, отражения и деформации………………......13
4.Задания для самостоятельного решения………………………..…...14
5.Заключение………………………………………………………………15
6. Выводы…………………………………………………………..………17
ВВЕДЕНИЕ
Преобразование графиков функции является одним из фундаментальных математических понятий, непосредственно связанные с практической деятельностью. В графиках отражены изменчивость и динамичность реального мира, взаимные отношения реальных объектов и явлений.
Функциональная линия является базовой тематикой, рассматриваемая в Основном и Едином государственных экзаменах. Так же многие математические понятия рассматриваются графическими методами. Например, к вадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Отсюда следует, что обучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.
Исследование функции дает возможность найти об ласть определения и область значения функции, обла сти убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Однако для построения графи ков многих функций можно использовать ряд методов, облегча ющие построение. Поэтому учащиеся должны иметь компетенции построения графиков по методическим схемам.
Выше сказанное определяет актуальность темы исследования.
Объектом исследования является изучение преобразование графиков функциональной линии в школьной математике.
Предмет исследования – процесс построение и преобразование графиков функции в общеобразовательной школе.
Цель исследования: образовательная - заключается в выявлении методической схемы построения и преобразования графиков функции; развивающая - развитие абстрактного, алгоритмического, логического мышления, пространственного воображения; воспитательная – воспитание графической культуры школьников, формирование навыков умственного труда.
Цели обусловили решение следующих задач:
1. Проанализировать учебно-методическую по исследуемой проблеме.
2. Выявить методические схемы преобразования графиков функции в школьном курсе математики.
3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в общеобразовательной школе , способствующие: осмысленному усвоению учебного материала; повышению познавательной активности учащихся; развитию их творческих способностей.
ГИПОТЕЗА исследования: формирование графических навыков в процессе изучения функций и воспитание графической культуры учащихся будет эффективным, если учащиеся владеют методической схемой построения и преобразования графиков функции в школьном курсе математики.
ГЛАВА I . ОБЗОР ЛИТЕРАТУРЫ ПО ТЕМЕ ПРОЕКТА.
При подготовке к проекту мы изучили следующую литературу:
Сивашинский, И. Х. Теоремы и задачи по алгебре, элементарным функциям - М., 2002. - 115 с.
Гельфанд, И. М., Глаголева, Е. Г., Шноль, Э. Э. Функции и графики (основные приемы) - М., 1985. - 120 с
В.З.Зайцев, В.В. Рыжков, М.И. Сканави. Элементарная математика- М., 2010(переиздание). - 590 с.
Кузьмин, М. К. Построение графика функции - Ж. Математика в школе. - 2003. - №5. - С. 61-62.
Шилов Г.Е. Как строить графики? - М., 1982.
Исаак Танатар. Геометрические преобразования графиков функций - МЦНМО, 2012
В отмечено, что умение с помощью графика «прочитать» поведение функции на некотором множестве находит применение не только в курсе математики, но и в любой практической деятельности человека, в которой ему приходится иметь дело с теми или иными графическими изображениями зависимостей. Поэтому учащиеся должны уметь по графику функции определить некоторые ее свойства.
В строго изложен теоретический материал преобразования графиков. Сопровождается методика иллюстрацией рисунками, различной сложности примерами и их решениями, что дает возможность углублено расширить знания и построении графиков сложных функций.
Представляет электронный учебный курс, объем и содержание которого соответствуют требованиям к курсу математики старших классов средней школы. Теоретический материал подкреплен графическими анимационными иллюстрациями, которые дают наглядные представления об изучаемой теме. Курс включает три модуля: модуль изучения теоретического материала, модуль самопроверки и модуль контроля знаний.
Из , , использованы для эмпирической части проекта методические схемы построения графиков, примеры для самостоятельной работы.
Выводы к 1 главе
Изучение учебно-методической литературы позволило:
1. Выявить методическую схему изучения, построения и преобразования графиков функции в школьном курсе математики.
2. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в школьной математике, способствующие:
осмысленному усвоению учебного материала;
повышению познавательной активности учащихся;
развитию их творческих способностей.
3. показать, что функциональная линия оказывает существенное влияние при изучении различных понятий в математике.
Глава 2. ЭМПИРИЧЕСКАЯ ЧАСТЬ
В этой главе мы рассмотрим основные методы преобразования графиков функций, дадим методические схемы построения различных комбинаций графиков для различных функций.
2.1. ОСНОВНЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ
Перенос вдоль оси ординат
f ( x ) f ( x )+ b .
Для построения графика функции y = f ( x ) + b следу ет:
1. построить график функции y = f ( x )
2. перенести ось абсцисс на | b | единиц вверх при b >0 или на | b | еди ниц вниз при b < 0. Полученный в новой системе коор динат график является графиком функции y = f ( x ) + b .

2. Перенос вдоль оси абсцисс
f ( x ) f ( x + a ) .
y = f ( x + a ) следу ет:

3. Построение графика функции вида y = f (- x )
f (x ) f (- x ).
Для построения графика функции y = f ( - х) следует:
построить график функции y = f ( x )
отразить его отно сительно оси ординат
полученный график является графиком функции y = f ( - х).

4. Построение графика функции вида у = - f ( x )
f ( x ) - f ( x )
- f ( x ) следует:
построить график функции y = f ( x )
отразить его относительно оси абсцисс

2.2. Построение графиков четной и нечетной функций
При построении графиков четной и нечетной функции удобно пользоваться следующими свойствами:
1.График четной функции симмет ричен относительно оси ординат.
2. График нечетной функции симметричен относительно начала координат.
Для построения графиков четной и нечетной функции достаточно построить только правую ветвь графика для положительных значений аргумента. Левая ветвь достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.
Для построения графика четной функции y = f ( x ) сле дует:
построить ветвь графика этой функции только в об ласти положительных значений аргумента х≥О.
О тразить этот ветвь относительно оси ординат

Для построения графика нечетной функции y = f ( x ) следует:
строить ветвь графика этой функции только в области положительных значений аргумента (х≥0).
О тразить этот ветвь относительно начало координат в область отрицательных значений х.

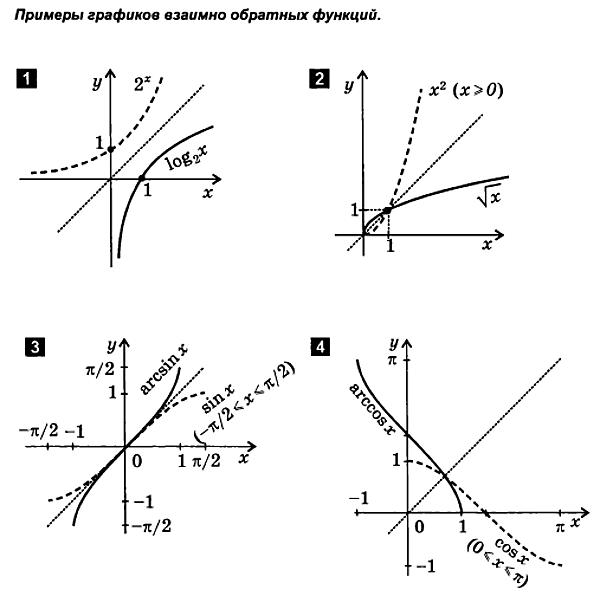
2.3. Построение графика обратной функции
Как уже отмечалось, прямая и обратная функции вы ражают одну и ту же зависимость между переменными х и у, с тем только отличием, что в обратной функции эти переменные поменялись ролями, что равносильно изме нению обозначений осей координат. Поэтому график обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т. е. относительно прямой у = х. Таким образом, получаем следующее правило.
Для построения графика функции у = (х), обратной по отношению к функции y = f ( x ), следует построить график y = f ( x ) и отразить его относительно прямой у = х.
2.4. Деформация (сжатие и растяжение) графиков
1. Сжатие (растяжение) графика вдоль оси ординат
f ( x ) A ∙ f ( x ).
Для построения графика функции y = A ∙ f ( x ) следует:

8. Сжатие (растяжение) графика вдоль оси абсцисс
f ( x )
Для построения графика функции у = f ( x ) следует:
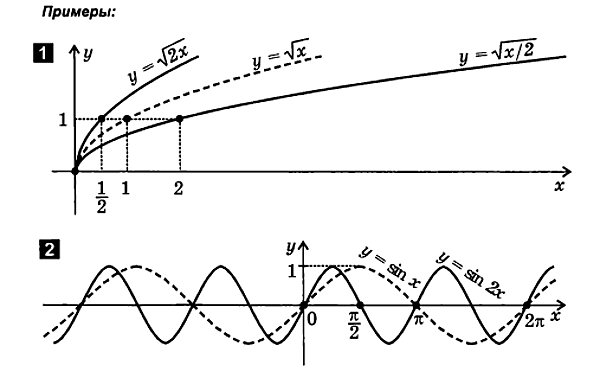
2.5. Комбинация переноса, отражения и деформации
Очень часто при построении графиков функций при меняют комбинацию приемов .
Последовательное применение ряда таких приемов поз воляет существенно упростить построение графика ис ходной функции и нередко свести его в конце концов к построению одной из простейших элементарных функ ций. Рассмотрим, как с учетом изложенного следует строить графики функций.
Отметим, что поря док упрощения целесообразно проводить в следующей последователь ности.
Использование четности или нечетности функции.
Перенос осей.
Отражение и деформация.
Построение же графика выполняется в обратной последовательности.
Пример.
Построить график функции
![]()
Построение проведем по следующим шагам:
1. построим график натурального логарифма :
2. сожмём
к оси
OY
в 2 раза:
;
3.
отобразим симметрично
относительно оси
OY
:
;
4. сдвинем вдоль оси
OX
на
(!!!) вправо:
![]() :
:

5. отобразим симметрично относительно оси
OX
:
;
6. сдвинем
вдоль оси
OY
на 3 единицы вверх:
![]() :
:

ПРИМЕРЫ ПОСТРОЕНИЯ и ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ
Пример 1. Построить график функции .
Сначала изобразим график синуса, его период равен :

график функции получается путём сжатия графика к оси ординат в два раза. log .
Построить график функции у = 2 cos х.
Построить график функции y = sin x .
ЗАКЛЮЧЕНИЕ
Во время работы над проектной работой были проанализирована различная учебно-методическая литература по данной проблеме. Результаты исследования позволили выявить наиболее характерные положительные стороны изучения , построения и преобразования графиков функции в школьном курсе математики
Основной целью проекта является формирование у учащихся умений и навыков в чтении и выполнении чертежей, в формировании у них рациональных приемов самостоятельной деятельности.
Необходимость усовершенствования графического образования в целом диктуется не только современными требованиями производства, но и ролью графики в развитии технического мышления и познавательных способностей учащихся. Способность человека к переработке графической информации является одним из показателей его умственного развития. Поэтому графическая подготовка должна стать неотъемлемым элементом общеобразовательной подготовки.
Выводы
Таким образом, разработанный проект « Построение и преобразование графиков функции», посвященный одному из центральных понятий математики - функциональной зависимости, ориентирован на систематизацию и расширение знаний учащихся. Изучение конкретных способов преобразования графиков функций проводится аналитико-графическим путем по строгим методическим схемам. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для проведения занятий могут использоваться разнообразные формы и методы организации и обучения.
Научно-исследовательская работа учащихся по теме:
«Применение линейной функции в решении задач»
МКОУ «Богучарская средняя общеобразовательная школа №1»
Научно-исследовательская работа по математике.
Тема: «Применение графика линейной функции к решению задач»
7 «В» класс
Руководитель:Фоменко Ольга Михайловна
город Богучар
1.Введение………………………………………………………………… 2
2.Основная часть……………………………………………………………3-11
2.1 Методика решения текстовых задач с помощью графиков линейной функции
2.2Решение текстовых задач на движение с помощью графиков
3.Заключение…………………………………………………………………11
4.Литература………………………………………………………………….12
ВВЕДЕНИЕ.
« Алгебра.7 класс» рассматриваются задачи, в которых по заданному графику необходимо ответить на ряд вопросов.
Например:
№332 Дачник отправился из дома на автомобиле в поселок. Сначала он ехал по шоссе,а затем по проселочной дороге, сбавив при этом скорость. График движения дачника изображен на рисунке. Ответьте на вопросы:
а)сколько времени ехал дачник по шоссе и сколько километров он проехал; какая скорость автомобиля была на этом участке пути;
б)сколько времени ехал дачник по проселочной дороге и сколько километров он проехал; какова была скорость автомобиля на этом участке;
в) за какое время дачник проехал весь путь от дома до поселка?
В ходе поиска материала по этой теме в литературе и Интернете я для себя открыла, что в мире в линейной зависимости находятся многие физические, и даже общественные и экономические явления и процессы, но я остановилась на движении, как наиболее нам знакомом и популярном среди всех. В проекте я описала текстовые задачи и способы их решения с помощью графиков линейной функции.
Гипотеза: с помощью графиков можно не только получить наглядные представления о свойствах функции, познакомиться со свойствами линейной функции и её частного вида, прямой пропорциональности, но и решать текстовые задачи.
Целью моего исследования стало изучение применения графиков линейной функции в решении текстовых задач на движение. В связи с осуществлением этих целей были выдвинуты следующие задачи:
Изучить методику решения текстовых задач на движение с помощью графиков линейной функции;
Научиться решать задачи на движение данным методом;
Сделать сравнительные выводы о достоинствах и недостатках решения задач с помощью графиков линейной функции.
Объект исследования: график линейной функции.
Метод исследования:
Теоретический (изучение и анализ),системно-поисковый, практический.
Основная часть.
В своем исследовании я решила попробовать дать графическое толкование задач на движение, представленных в нашем учебнике, затем по графику ответить на поставленный вопрос задачи. Для такого приёма решения взяла задачи с прямолинейным равномерным движением на одном участке пути. Оказалось, что многие задачи таким способом решаются проще, нежели обычным способом с помощью уравнения. Единственный недостаток этого приёма: для точного получения ответа на вопрос задачи, надо суметь правильно выбрать масштаб единиц измерения на осях координат. Большую роль в правильном выборе такого масштаба играет опыт нарешивания. Поэтому, чтобы овладеть искусством решения задач с помощью графиков, мне пришлось рассмотреть их в большом количестве.
задать систему координат sOt с осью абсцисс Ot и осью ординат Os . Для этого по условию задачи надо выбрать начало отсчета: начало движения объекта или из нескольких объектов избирается тот, который начал двигаться раньше или прошел большее расстояние. По оси абсцисс отметить интервалы времени в его единицах измерения, а по оси ординат отметить расстояние в выбранном масштабе его единиц измерения.
Точки на координатной плоскости должны быть отмечены в соответствии с масштабом по условию задачи, и линии должны быть построены аккуратно. От этого зависит точность решения задачи. Поэтому очень важно удачно выбрать масштаб делений на осях координат: его надо подобрать таким образом, чтобы координаты точек определялись более точно и, по возможности, располагались в узловых точках, т.е. в пересечениях делений осей координат. Иногда полезно за единичный отрезок на оси абсцисс брать количество клеток, кратное условиям задачи относительно времени, а на оси ординат – количество клеток, кратное условиям задачи относительно расстояния. Например, 12мин по времени требуют выбора числа клеток кратное 5, т.к. 12 мин составляет пятую часть часа.
Решение текстовых задач на движение с помощью графиков
Ответ: 9 км.

Решение с помощью уравнения:
х/12ч. – время от А до В
х/18ч. – время обратно
Ответ:9 км
Задача 2.(№ 156 в учебнике Ю.Н.Макарычева «Алгебра 7».)
По шоссе идут две машины с одной и той же скоростью. Если первая увеличит скорость на 10км/ч, а вторая уменьшит на 10км/ч, то первая за 2 часа пройдёт столько же, сколько вторая за 3 часа. С какой скоростью идут автомашины?
Решение с помощью уравнения:
Пусть х км/ч скорость машин;
(х+10) и (х-10) соответственно скорости после увеличения и уменьшения;
2(х+10)=3(х-10)
Ответ: 50км/ч
Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOt c осью абсцисс Оt , на которой отметим интервалы времени движения, и осью ординат Os , на которой отметим расстояние, пройденное автомашинами
2. Нанесём деления в масштабе по оси абсцисс – один час в 5 клетках (в 1 клетке – 12 мин); по оси ординат наносим деления, но не указываем масштаб.
3. Построим линию движения первой машиныI : начало движения в точке с
4. Построим линию движения второй машиныII : начало движения в точке с координатой (0;0). Далее отметим произвольную точку (3;s 1) на плоскости, т.к. машина с новой скоростью была в пути 3 часа.
4. Определим скорость машин v до её изменения. Обозначим разность ординат точек, лежащих на прямых с абсциссой 1, значком ∆s . По условию этому отрезку соответствует длина (10+10) км, т.к. у одной из них скорость уменьшилась, а у другой скорость увеличилась на 10км/ч. Значит, линия движения машин до изменения скорости должна быть равноудалена от линийI и II и расположена на координатной плоскости между ними.. По графику Δs =2кл. соответствует 20км, v =5 кл., значит, решим пропорцию v = 50км/ч.
Ответ: 50км/ч.
Задача 3
Решение с помощью графика линейной функции:
отсчёта является пристань М

отметим точку N (0; 162).
Ответ: 2ч 20мин.
Решение с помощью уравнения:
162 -45(x +0,75)-36x =0
162-45x – 33,75 -36x =0
81x =128,25
2) ![]()
Ответ: 2ч 20мин.
Задача 4.
Из пункта A выехал велосипедист. Одновременно вслед за ним из пункта B , отстоящего от A на расстоянии 20км, выехал мотоциклист 16км/ч. Велосипедист ехал со скоростью 12км/ч. На каком расстоянии от пункта A мотоциклист догонит велосипедиста?
Решение с помощью графика линейной функции:
1.Зададим координатную плоскость sOt с осью абсцисс Ot , на которой отметим интервалы времени движения, и ось ординат Os , на которой будем отмечать расстояние, пройденное мотоциклистом и велосипедистом
2. Нанесём деления в масштабе: по оси ординат – в 2 клетках 8 км; по оси абсцисс–в 2клетках –1ч.
3. Построим линию движения мотоциклиста II : начало его движения отметим в начале координат В(0;0). Мотоциклист ехал со скоростью 16км/ч, значит, прямаяII должна пройти через точку с координатами (1;16).

4.Построим линию движения велосипедистаI : её начало будет в точке А(0;20), т.к. пункт B расположен от пункта A на расстоянии 20км, и он выехал одновременно с мотоциклистом. Велосипедист ехал со скоростью 12км/ч, значит, прямая I должна пройти через точку с координатами (1;32).
5. Найдем Р (5; 80) – точку пересечения прямых I и II , отражающих движение мотоциклиста и велосипедиста: ее ордината покажет расстояние от пункта В, на котором мотоциклист догонит велосипедиста.
Р(5; 80) |=s = 80, |=80 – 20 = 60(км) – расстояние от пункта А, на котором мотоциклист догонит велосипедиста..
Ответ: 60км.
Решение с помощью уравнения:
Пусть x км расстояние от пункта А до места встречи
x /12 время велосипедиста
(x +20)/16 время мотоциклиста
x /12=(x +20)/16
16x =12x +240
4x =240
x =60
Ответ: 60 км
Задача 5.
Расстояние между городами мотоциклист проехал за 2ч, а велосипедист за 5 ч. Скорость велосипедиста на 18км/ч меньше скорости мотоциклиста. Найдите скорости велосипедиста и мотоциклиста и расстояние между городами.
Решение с помощью графика линейной функции:

1. Зададим координатную плоскость sOt с осью абсцисс Ot , на которой отметим интервалы времени движения, и ось ординат Os , на которой отметим расстояние.
2. Нанесем деление по оси абсцисс в 2х клетках 1 ч. По оси ординат расстояние оставим без делений.
3. Проведем линию движения I велосипедиста за 5 часов и линию движения мотоциклиста II за 2 часа. Конец обеих линий должен иметь одну ординату.
4. Проведём отрезок с абсциссой 1 между линиями I и II . Длина этого отрезка отражает расстояние равное 18км. Из чертежа получаем, что 3 клетки равны 18 км, значит, в 1 клетке 6км.
5. Тогда, по графику определяем скорость велосипедиста равна12 км/ч, скорость мотоциклиста равна 30 км/ч, расстояние между городами-60 км.
Решение с помощью уравнения:
Пусть x км/ч скорость велосипедиста, тогда(x +18) км/ч скорость мотоциклиста
2(x +18)=5x
2x +36=5x
x =12
2) 12+18=30(км/ч) скорость мотоциклиста
3) (км) расстояние между городами
Ответ: 12 км/ч; 30 км/ч; 60 км
Ответ: 60км.
Задача 6.
По течению реки лодка за 3ч 20мин проходит расстояние 30км, а против течения за 4ч – расстояние 28км. Какое расстояние по озеру пройдет лодка за 1,5ч?
Решение с помощью графика линейной функции:
1.Зададим координатную плоскость sOt с осью абсцисс Ot , на которой отметим интервалы времени движения, и ось ординат Os , на которой отметим расстояние, пройденное лодкой
2. Нанесём деления в масштабе: по оси ординат – в двух клетках 4км; по оси абсцисс– в 6 клетках – 1ч (в 1 клетке – 10 мин.), т.к. по условию задачи дано время с минутами.
3. Построим линию движения лодки по течению рекиI : начало линии будет в точке с координатой (0;0). Лодка плывает 30км за 3ч 20мин, значит, линия должна пройти через точку с координатой (;30), т.к. 3ч 20мин. = ч.

4. Построим линию движения лодки против течения рекиII : начало движения возьмём в точке с координатой (0;0). Лодка плывет 28км за 4ч, значит, прямая движения должна пройти через точку с координатой (4;28).
5. Построим линию движения лодки по озеру: начало движения возьмём в точке с координатой (0; 0). Линия собственного движения лодки должна будет располагаться равноудалённо и между линиями движения лодки по реке. Значит, мы должны отрезок, состоящий из всех точек с абсциссой 1 между линиями движения по реке, поделить пополам и отметить его середину. От (0; 0) через эту отмеченную точку проведём луч, который и будет линией движения по озеру.
6. По условию задачи надо найти расстояние, пройденное лодкой по озеру за 1,5ч, значит, мы должны определить на этой линии ординату точки с абсциссой t = 1,5, |=s = 12, |= 12км пройдёт лодка по озеру за 1,5 часа.
Ответ: 12км.
Решение с помощью системы уравнений:
Пусть x км/ч скорость по озеру, а у км/ч скорость реки
Ответ: 12км.
Задача 7.
Катер проходит по течению реки 34 км за то же время, что и 26 км против течения. Собственная скорость катера равна 15км/ч. Найдите скорость течения реки.
Решение с помощью графика линейной функции:
1.Зададим координатную плоскость sOt с осью абсцисс Ot , на которой отметим интервалы времени движения, и ось ординат Os , на которой отметим расстояние, пройденное лодкой.
2. Нанесём деления в масштабе: по оси ординат – в 1 клетке 1км; по оси абсцисс время оставим без делений.
3. Построим линию I движения лодки по течению реки из 0км до точки в 34 км: начало линии будет в точке с координатой (0;0).Вторая координата будет (x ; 34).
4. Построим линию II движения лодки против течения реки из 0км до точки в 26 км: начало линии будет в точке с координатой (0;0).Вторая координата будет (x ; 26).
5. Проведем луч III из начала координат (0; 0) через середину произвольного отрезка, состоящего из всех точек с одинаковой абсциссой между двумя линиями движения I и II . Этот луч будет отражать собственное движение лодки, т.к. собственная скорость катера есть среднее арифметическое 2х скоростей по течению и против течения реки. На полученном луче найдём точку с ординатой 15, т.к. собственная скорость лодки 15км/ч. Абсцисса найденной точки будет соответствовать делению в 1 час.
6. Чтобы найти скорость течения реки, достаточно найти длину отрезка с абсциссой 1 от линии III до линии II . Скорость течения реки - 2км/ ч.
Ответ: 2км/ ч.
Решение с помощью уравнения:
Скорость течения реки x км/ч
34/(15+х)=26/(15-х) Решая пропорцию, получим:
Ответ: 2км/ ч.
Заключение.
Достоинства:
Можно кратко записать задачи;
Недостатки:
ЛИТЕРАТУРА.
1. Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б., Алгебра: Учебник для 7 класса общеобразовательных учреждений, «Просвещение», М., 2000.
2.Булынин В., Применение графических методов при решении текстовых задач, учебно-методическая газета «Математика», № 14, 2005.
3. Звавич Л.И.Дидактические материалы по алгебре для 7 класса.
На уроках алгебры в 7 классе я познакомилась с темой «Линейная функция. Взаимное расположение графиков линейных функций». Я научилась строить графики линейной функции, узнала её свойства, научилась по заданным формулам определять взаимное расположение графиков. Я обратила внимание, что в учебнике Ю.Н.Макарычева
« Алгебра.7 класс» рассматриваются задачи, в которых по заданному графику необходимо ответить на ряд вопросов. Пример такой задачи представлен на слайде.
По заданному графику можно определить, что
И у меня возник вопрос, можно ли решать задачи на движение не по действиям или при помощи уравнений, а применить для этого графики линейной функции?
Гипотеза,цели и задачи представлены на слайде
В своем исследовании я решила попробовать дать графическое толкование задач на движение, представленных в нашем учебнике, затем по графику ответить на поставленный вопрос задачи. Для такого приёма решения взяла задачи с прямолинейным равномерным движением на одном участке пути.
Оказалось, что многие задачи решаются таким способом. Единственный недостаток этого приёма: для точного получения ответа на вопрос задачи, надо суметь правильно выбрать масштаб единиц измерения на осях координат. Большую роль в правильном выборе такого масштаба играет опыт нарешивания. Поэтому, чтобы овладеть искусством решения задач с помощью графиков, мне пришлось рассмотреть их в большом количестве.
Методика решения текстовых задач с помощью графиков линейной функции.
Для того, чтобы решить текстовую задачу с помощью графиков линейной функции, надо:
задать систему координат Для этого по условию задачи надо выбрать начало отсчета: начало движения объекта или из нескольких объектов избирается тот, который начал двигаться раньше или прошел большее расстояние. По оси абсцисс отметить интервалы времени в его единицах измерения, а по оси ординат отметить расстояние в выбранном масштабе его единиц измерения.
Провести линии движения каждого из объектов, указанных в условии задачи, через координаты хотя бы двух точек прямых. Обычно скорость объекта даёт информацию о прохождении расстояния за одну единицу времени от начала его движения. Если объект начинает двигаться позже, то точка начала его движения смещена на заданное число единиц вправо от начала отсчета вдоль оси абсцисс. Если объект начинает двигаться с места, удаленного от начала отсчета на определённое расстояние, то точка начала его движения смещена вверх вдоль оси ординат.
Место встречи нескольких объектов на координатной плоскости обозначено точкой пересечения прямых, изображающих их движение, значит, координаты этой точки дают информацию о времени встречи и удаленности места встречи от начала отсчета.
Разность скоростей движения двух объектов определяется длиной отрезка, состоящего из всех точек с абсциссой 1, расположенных между линиями движения этих объектов.
Точки на координатной плоскости должны быть отмечены в соответствии с масштабом по условию задачи, и линии должны быть построены аккуратно. От этого зависит точность решения задачи.
Задача 1.(№ 673 в учебнике Ю.Н.Макарычева «Алгебра 7».)
Велосипедист проехал путь АВ со скоростью 12 км/ч. Возвращаясь, он развил скорость 18 км/ч и затратил на обратный путь на 15 мин меньше, чем на путь из А в В. Сколько километров из А в В.
Решение с помощью уравнения:
Пусть х км – расстояние от А до В.
х/12ч. – время от А до В
х/18ч. – время обратно
Так как на обратный путь он затратил на 15 минут меньше, то составим уравнение
Ответ:9 км
Решение с помощью графика линейной функции:
1. Зададим координатную плоскость sOtc осью абсцисс Оt , на которой отметим интервалы времени движения, и осью ординат Os , на которой отметим расстояние.
2. Нанесём деления в масштабе: по оси ординат – в одной клетке 3 км; по оси абсцисс – один час в 4 клетках (в 1 клетке – 15 мин).
3. Построим линию движения туда: начало движения отметим точкой (0;0). Велосипедист ехал со скоростью 12км/ч, значит, прямая должна пройти через точку (1;12).
4. Построим линию движения обратно: конец линии отметим точкой (; 0), т.к. велосипедист затратил на обратный путь на 15 минут меньше. Он ехал со скоростью 18км/ч, значит, следующая точка прямой имеет координату (;18).
5. Отметим (; 9) - точку пересечения прямых: её ордината покажет расстояние: s = 9
Ответ: 9 км.
Задача 2 (№ 757 в учебнике Ю.Н.Макарычева« Алгебра 7»)
Расстояние между пристанями M и N равно 162км. От пристани M отошел теплоход со скоростью 45км/ч. Через 45 мин от пристани N навстречу ему отошел другой теплоход, скорость которого 36км/ч. Через сколько часов после отправления первого теплохода они встретятся?
Решение с помощью уравнения:
Пусть через x часов произойдет встреча
162 -45(x +0,75)-36x =0
162-45x – 33,75 -36x =0
81x =128,25
2) ![]()
Ответ: 2ч 20мин.
Решение с помощью графика линейной функции:
1. Зададим координатную плоскость sOt с осью абсцисс Ot , на которой отметим интервалы времени движения, и ось ординат Os , на которой
отметим расстояние от пристани M до пристани N , равное 162км. Началом
отсчёта является пристань М
2. Нанесём деления в масштабе: по оси ординат – в двух клетках 18км; по оси абсцисс–один час в 6 клетках (в 1 клетке–10мин.), т.к. в условии задачи указано время в минутах.
отметим точку N (0; 162).
3. Построим линию движения первого теплохода I : начало его движения будет в точке с координатами (0;0). Первый теплоход плыл со скоростью 45км/ч, значит, прямая должна пройти через точку с координатами (1;45).
4. Построим линию движения второго теплоходаII : начало движения будет в точке с
координатами (; 162), так как он вышел из пункта N , удалённого от М на 162км, на 45мин. позже первого, а 45мин. = ч. Второй теплоход плыл со скоростью 36км/ч, значит, прямая должна пройти через точку (; 126), так как второй теплоход вышел в направлении пункта М: 162 – 36 = 126(км).
5. Точкой пересечения прямыхI и II является точка А (;108). Абсцисса точки показывает время, через которое после отправления первого теплохода они встретились: t =, |=ч = 2ч20мин. – время встречи двух теплоходов после выхода первого теплохода.
Ответ: 2ч 20мин.
Заключение.
В конце исследования я смогла выявить достоинства и недостатки решения задач графическим способом.
Достоинства:
Можно кратко записать задачи;
Вполне легко работать с маленькими числами.
Недостатки:
Сложно работать с большими числами.

ОСР. «Решение уравнений с помощью графиков».
Задание:
1) Опорный конспект.
Графиком называется множество точек координатной плоскости, у которых значения x и y
связаны некоторой зависимостью и каждому значению x соответствует единственное значение y.
Графический способ один из самых удобных и наглядных способов представления и анализа
информации.
На практике довольно часто оказывается полезным графический метод решения уравнений. Он
заключается в следующем: для решения уравнений f(x)=0 строят график функции y=f(x) и находят
абсциссы точек пересечения графика с осью Оx: эти абсциссы и являются корнями уравнения.
Алгоритм решения уравнений графическим способом
Чтобы решить графически уравнение вида f(х) = g(х), нужно:
1.Построить в одной координатной плоскости графики функции:
у = f(х) и у = g(х).
2. Найти точки пересечения этих графиков.
3. Указать абсциссу каждой из этих пересечения.
4. Записать ответ.
Довольно просто решать графически систему уравнений, так как каждое
уравнение системы на координатной плоскости представляет какую то
линию.
Построив графики этих уравнений и найдя координаты точек их
пересечения (если они существуют), мы получим искомое решение.
Графическое решение неравенств, сводится к отысканию таких точек x,
при которых один график лежит выше или ниже другого.
Примеры:
№ 1. Решите уравнение
x
4
5
x

точки
пересечени
я
графиков
функций
№
2.
Решите
является
рисунок
абсцисса
1
.
уравнения
5
см.
:
х
х
4
Решением
у
уи
Проверка
1
4
15
4
4
верно
Ответ
.1:
уравнение
x
3
3
x

Решением
уравнения
является
у
3
х
уи
3
х
см.
рисунок
абсцисса
.
2
точки
пересечени
я
графиков
функций
№3. Ре
1
3
Проверка
:
3
1
верно
1:
33
Ответ
.
шить уравнение
Решение: Построим графики функций
и y = x
Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).
Ответ: корней нет.
№4.Найти значение выражения х + у,если (х
;у
является решением системы уравнений.
Решение:
влево.
параллельный перенос на 1 единицу
параллельный перенос на 2 единицы влево.
= 1, у
=1
+ у
=0.
х
х
Ответ: 0.

№5. Решите неравенство
Ответ: х>2.
>12 1,5х. №6. Решите неравенство
. Oтвет: х>0.
№7. Решить уравнение sinx + cosx=1. Построим графики функций y=sinx u y=1cosx.(рисунок 5) Из
графика видно, что уравнение имеет 2 решения: х=2 п,где пЄZ и х= /2+2 k,где kЄZ.
π
π
π
2
sin x(
1
cos x(
6
4
2
1
2
2
1
1
0
x
2
4
6
2
№8.Решить уравнение: 3x = (х1) 2 + 3
Решение: применяем функциональный метод решения уравнений:
т.к. данная система имеет единственное решение, то методом подбора находим х=1

Ответ: 1.
№9.Решить неравенство: сos x 1 + 3x
Решение:
Ответ: (
;
).
№10. Решить уравнение
В нашем случае функция
возрастает при х>0, а функция y = 3 – x убывает при
всех значениях х, в том числе и при х>0, значит,
уравнение
корня. Заметим, что при х = 2 уравнение обращается
в верное равенство, так как
имеет не более одного
.
Ответ: 2 .
2)Решить задание:
1)Есть ли корень у уравнения и если есть, то положительный он или отрицательный?
а)
; б)
, в) 6х =1/6, г)
.
2) Решить графическим методом уравнение
.
1
3
х
3
х
3) Решите графическим методом уравнения:
а)
б)
.
3
х
3
х
5
1
2
х

4)На рисунке изображен график функции y=f(x).
1) 1 2) 6 3) 7 4) 8
5) На каком из рисунков изображен график функции
?
у
log
x
1
2
1) у 2) у 3) у 4)
у
1 1 1
6) График какой функции изображен на рисунке?
1) у = 2х1,5; 2) у = 2х – 2;
3) у = 2х – 3; 4) у = 2х – 2.
7)График какой функции изображен на рисунке?
1) у = sinx; 2)
у
sin
x
6
; 3)
у
sin
x
3
; 4)
.
у
sin
x
6
8) На рисунке изображен график функций
y = f (x) и y = g (x), заданный на промежутке
[5;6]. Укажите те значения х, для которых
выполняется неравенство g (x)
y
у
)(xg
f (x) 1
1) [5; 0] 2) [5; 2]
0 1 x
3) [2; 2] 4)
9) На рисунке изображен график функции y=f(x).
Найдите количество целых корней уравнения f(x)= 0.
1) 3 2) 4 3) 2 4) 1
)(xf
у
10) На рисунке изображен график функции y=f(x).
Найдите количество целых корней уравнения f(x)+2= 0.
1) 3 2) 5 3) 4 4) 1
Графическое решение квадратного уравнения Закрепить умение строить графики различных функций; Формировать умение решать квадратные уравнения графическим способом. г. Брдск 2009 Муниципальное общеобразовательное учреждение – Экономический лицей Обобщающий урок по теме «Квадратичная функция», алгебра 8 класс учитель Федосеева Т.М.
Построение графика квадратичной функции Определить направление ветвей: a>0 ветви вверх; a 0 ветви вверх; a"> 0 ветви вверх; a"> 0 ветви вверх; a" title="Построение графика квадратичной функции Определить направление ветвей: a>0 ветви вверх; a"> title="Построение графика квадратичной функции Определить направление ветвей: a>0 ветви вверх; a">
0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк" title="Построим график функции у=х 2 -2х-3 с помощью алгоритма: 1) а=1>0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк" class="link_thumb"> 3 Построим график функции у=х 2 -2х-3 с помощью алгоритма: 1) а=1>0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точки пересечения с осью ОХ: х 1 =-1; х 2 =3 1 способ решения уравнения х 2 -2х-3=0 y x Решить уравнение х 2 +2х-3=0 0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк"> 0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точки пересечения с осью ОХ: х 1 =-1; х 2 =3 1 способ решения уравнения х 2 -2х-3=0 y x 0 1 -4 23 Решить уравнение х 2 +2х-3=0"> 0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк" title="Построим график функции у=х 2 -2х-3 с помощью алгоритма: 1) а=1>0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк"> title="Построим график функции у=х 2 -2х-3 с помощью алгоритма: 1) а=1>0 ветви направлены вверх; 2) вершина у о =у(1)=1-2-3=-4 А(1;-4) х=1 – ось параболы Контрольные точки: (0: -3), (3; 0) и им симметричные относительно оси х=1 Строим параболу. Находим точк">
Второй способ: а). Уравнение х 2 -2х-3=0 разобьём на части х 2 = 2х+3 Запишем две функции у= х 2 ; у=2х+3 Строим графики данных функций в одной системе координат. Абсциссы точек пересечения являются корнями уравнения. 0 1 х у Решить уравнение х 2 +2х-3=0

Третий способ: х 2 -3 = 2х y= х 2 -3; y=2х Строим графики данных функций в одной системе координат. Абсциссы точек пересечения являются корнями уравнения. 0 1 х у Решить уравнение х 2 +2х-3=0


