погрешность измерения
Отклонение результата измерения от истинного (действительного) значения измеряемой величины.
Синонимом термина погрешность измерения является термин ошибка измерения , применять который не рекомендуется как менее удачный
Составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
Примечание - В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодические и погрешности, изменяющиеся по сложному закону .
Постоянные погрешности - погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности - непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности - погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей
Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений
погрешность метода
Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений.
Примечания
1 Вследствие упрощений, принятых в уравнениях для измерений, нередко возникают существенные погрешности, для компенсации действия которых следует вводить поправки. Погрешность метода иногда называют теоретической погрешностью .
2 Иногда погрешность метода может проявляться как случайная
Составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Примечание - Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
субъективная погрешность
Составляющая систематической погрешности измерений, обусловленная индивидуальными особенностями оператора.
Примечания
1 Встречаются операторы, которые систематически опаздывают (или опережают) снимать отсчеты показаний средств измерений
2 Иногда субъективную погрешность называют личной погрешностью или личной разностью
НСП
Составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины
абсолютная погрешность
Погрешность измерения, выраженная в единицах измеряемой величины
Значение погрешности без учета ее знака (модуль погрешности)
Примечание - Необходимо различать термины абсолютная погрешность и абсолютное значение погрешности
относительная погрешность
Погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
рассеяние результатов;
рассеяние
Несовпадение результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обусловленное действием случайных погрешностей.
Примечания
1 Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
2 Оценками рассеяния результатов в ряду измерений могут быть:
размах,
средняя арифметическая погрешность (по модулю),
средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение),
доверительные границы погрешности (доверительная граница или доверительная погрешность)
размах
Оценка R n рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле
R n = X max - X min
где X max и X min - наибольшее и наименьшее значения физической величины в данном ряду измерений.
Примечание - Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер
средняя квадратическая погрешность измерений;
средняя квадратическая погрешность;
СКП
Оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения
где xi - результат i-го единичного измерения;
X - среднее арифметическое значение измеряемой величины из n единичных результатов.
Примечание - На практике широко распространен термин среднее квадратическое отклонение - (СКО). Под отклонением в соответствии с формулой (9.6) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В метрологии, как отмечено в 9.1, это отклонение называется погрешностью измерений. Если в результаты измерений введены поправки на действие систематических погрешностей, то отклонения представляют собой случайные погрешности. Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин "погрешность измерения", целесообразно применять термин "средняя квадратическая погрешность". При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений
средняя квадратическая погрешность среднего арифметического;
средняя квадратическая погрешность ;
СКП
Оценка Sx случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений, вычисляемая по формуле
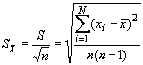
, (9.7)
где S - средняя квадратическая погрешность результатов единичных измерений, полученная из ряда равноточных измерений; n - число единичных измерений в ряду
доверительные границы погрешности;
доверительные границы
Наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
2 При симметричных границах термин может применяться в единственном числе - доверительная граница .
3 Иногда вместо термина доверительная граница применяют термин доверительная погрешность или погрешность при данной доверительной вероятности
9.17 поправка
Значение величины, вводимое в неисправленный результат измерения с целью исключения составляющих систематической погрешности.
Примечание - Знак поправки противоположен знаку погрешности. Поправку, прибавляемую к номинальному значению меры, называют поправкой к значению меры ; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора
9 . 18 поправочный множитель
Числовой коэффициент, на который умножают неисправленный результат измерения с целью исключения влияния систематической погрешности.
Примечание - Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению величины
9 . 19 точность результата измерений ;
точность измерений
Одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание - Считают, что чем меньше погрешность измерения, тем больше его точность
9 . 20 неопределенность измерений ;
неопределенность
Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые можно приписать измеряемой величине.
Примечания
1 Определение взято из VIM-93 .
2 К определению в приведены примечания, из которых следует, что:
а) параметром может быть стандартное отклонение (или число, кратное ему) или половина интервала, имеющего указанный доверительный уровень;
б) неопределенность состоит (в основном) из многих составляющих. Некоторые из этих составляющих могут быть оценены экспериментальными стандартными отклонениями в статистически распределенной серии результатов измерений. Другие составляющие, которые также могут быть оценены стандартными отклонениями, базируются на данных эксперимента или другой информации
9 . 21 погрешность метода поверки
Погрешность применяемого метода передачи размера единицы при поверке
9 . 22 погрешность градуировки средства измерений ;
погрешность градуировки
Погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки
9 . 23 погрешность воспроизведения единицы физической величины ;
погрешность воспроизведения
Погрешность результата измерений, выполняемых при воспроизведении единицы физической величины.
Примечание - Погрешность воспроизведения единицы при помощи государственных эталонов обычно указывают в виде ее составляющих: неисключенной систематической погрешности; случайной погрешности; нестабильности за год
9 . 24 погрешность передачи размера единицы физической величины ;
погрешность передачи размера единицы
Погрешность результата измерений, выполняемых при передаче размера единицы.
Примечание - В погрешность передачи размера единицы входят как неисключенные систематические, так и случайные погрешности метода и средств измерений
9 . 25 статическая погрешность измерений ;
статическая погрешность
Погрешность результата измерений, свойственная условиям статического измерения
9 . 26 динамическая погрешность измерений ;
динамическая погрешность
Погрешность результата измерений, свойственная условиям динамического измерения
9 . 27 промах
Погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание - Иногда вместо термина "промах" применяют термин грубая погрешность измерений
9 . 28 предельная погрешность измерения в ряду измерений ;
предельная погрешность
Максимальная погрешность измерения (плюс, минус), допускаемая для данной измерительной задачи.
9 . 29 погрешность результата однократного измерения ;
погрешность измерения
Погрешность одного измерения (не входящего в ряд измерений), оцениваемая на основании известных погрешностей средства и метода измерений в данных условиях (измерений).
Пример - При однократном измерении микрометром какого-либо размера детали получено значение величины, равное 12,55 мм. При этом еще до измерения известно, что погрешность микрометра в данном диапазоне составляет ±0,01 мм, и погрешность метода (непосредственной оценки) в данном случае принята равной нулю. Следовательно, погрешность полученного результата будет равна ±0,01 мм в данных условиях измерений
9 . 30 суммарная средняя квадратическая погрешность результата измерений ;
суммарная погрешность результата;
суммарная погрешность
Погрешность результата измерений (состоящая из суммы случайных и неисключенных систематических погрешностей, принимаемых за случайные), вычисляемая по формуле
, (9.8)
где
Средняя квадратическая погрешность суммы неисключенных систематических погрешностей при равномерном распределении (принимаемых за случайные).
Примечание - Доверительные границы суммарной погрешности ( Δx) Σ могут быть вычислены по формуле
( Δx) Σ = ±t Σ S Σ (9.9)
где ; Θ - граница суммы неисключенных систематических погрешностей результата измерений, вычисляемая по формулам (9.2) или (9.3); t*Sx - доверительная граница погрешности результата измерений по 9.16
Время заряда
от 6,5 до 8,5 В
2.4 Определение положения точек земной поверхности с помощью геодезических спутниковых систем
Разработанные Федеральной службой геодезиии картографии России концепция и программа перехода топографо-геодезического производства на автономные методы спутниковых координатных определений изложены в работе Е. А. Жалковского, Г. В. Демьянова, В. И. Зубинского, П. Л. Макаренко, Г. А. Пьянкова «О концепции и программе перехода топографо-геодезического производства на автономные методы спутниковых координатных определений» (Геодезия и картография, 1998, № 5). Традиционные геодезические методы основаны на последовательном развитии геодезических сетей путем угловых и линейных измерений, требующих для обеспечения прямой видимости между смежными пунктами постройки геодезических знаков, сооружение которых потребовало около 80% средств, затраченных на создание существующих опорных сетей.
По сравнению с традиционными спутниковые методы ГЛОНАСС/GPS имеют следующие преимущества:
передача с высокой оперативностью и точностью координат практически на любые расстояния;
геодезические пункты можно располагать в благоприятных для их сохранности местах, так как не нужно обеспечивать взаимную видимость между пунктами и, следовательно, строить дорогостоящие геодезические знаки;
простота и высокий уровень автоматизации работ;
понижение требований к плотности исходной геодезической основы.
Реализация спутниковых технологий предусматривает построение следующих геодезических сетей:
фундаментальная астрономо-геодезическая сеть (ФАГС) - высшее звено координатного обеспечения; она должна обеспечивать оперативное воспроизведение общеземной геоцентрической системы координат, стабильность системы координат во времени, метрологическое, обеспечение высокоточных космических средств измерений;
высокоточная геодезическая сеть (ВГС), обеспечивающая распростра- нение на всю территорию страны общеземной геоцентрической системы координат и определение точных параметров взаимного ориентирования общеземной и референцной систем координат;
спутниковые геодезические сети 1-го класса (СГС-1).
Эти три класса сетей строго связаны между собой: ФАГС является опорой для ВГС, а ВГС - для СГС-1.
При построении ФАГС, ВГС и СГС-1 предусматривается привязка существующей ГГС к высшему классу спутниковых сетей, т. е. существующая ГГС будет сетью сгущения.
Пункты ФАГС располагаются на расстоянии 800-1000 км, их число - 50+70,10-15 пунктов должны быть постоянно действующими, а остальные - переопределяться группами через промежутки времени, зависящие от геодинамической активности региона.
Пространственное положение пунктов ФАГС определяется в общеземной системе координат с ошибкой положения пунктов относительно центра масс не более (2-3)10-8 R, где R - радиус Земли, ошибка взаимного положения пунктов ФАГС не более 2 см в плане и 3 см по высоте. Для обеспечения этой точности необходимо использовать весь комплекс существующих космических измерений (лазерных, радиоинтерферометрических и других).
ВГС является системой пунктов с расстоянием D = 150-300 км между ними, которые определяются относительными методами космической геодезии со средней квадратической ошибкой не более 3 мм + 5 10-8 D для плановых координат и 5 мм + 7 10-8 D - для геодезических высот.
СГС-1 состоят из системы легкодоступных пунктов с плотностью, достаточной для использования потребителями всевозможных спутниковых определений. СГС-1 определяются относительными методами космической геодезии со средними квадратическими ошибками: 3 мм + 10-7 D в плане и 5 мм + + 2 10-8 D по геодезической высоте для геодинамически активных регионов и 5 мм + 2 10-7. D в плане и 7мм + 3 10-7 D по высоте для остальных регионов. Среднее расстояние между пунктами СГС-1 равно 25-35 км. В экономически развитых районах пункты СГС-1 в зависимости от требований потребителей могут иметь большую плотность.
Постоянно действующие пункты ФАГС в основном создаются на базе действующих пунктов спутниковых (космических) наблюдений, астрономических обсерваторий, пунктов службы вращения Земли, радиоинтерферометрических комплексов со сверхдальними базами «Квазар», программы «Дельта» и др. На пунктах ФАГС предусматривают две программы наблюдений: постоянные наблюдения спутниковых систем ГЛОНАСС и GPS (включая и международные программы) и наблюдения других специализированных спутников и космических объектов согласно межведомственным программам построения ФАГС.
Следует заметить, что спутниковые технологии не всегда можно использовать при решении традиционных геодезических задач, например, недостаточна относительная точность определений на коротких расстояниях, ограничено использование GPS-методов в точной инженерной геодезии , процесс привязки ориентирных пунктов, легко решаемый в традиционной технологии, становится довольно сложным и дорогим, особенно в закрытой местности, в спутниковой технологии, так как объем спутниковых определений в этом случае возрастает более чем в два раза.
3. Погрешности геодезических измерений (теория и решение задач)
3.1 Геодезическое измерение, результат измерения, методы и условия измерений. Равноточные и неравноточные измерения
Измерением называется процесс сравнения некоторой физической величины с другой одноименной величиной, принятой за единицу меры.
Единица меры – значение физической величины, принятой для количественной оценки величины того же рода.
Результат измерений – это число, равное отношению измеряемой величины единицы меры.
Различают следующие виды геодезических измерений:
Линейные, в результате, которых получают наклонные иррациональные расстояния между заданными точками. Для этой цели применяют ленты, рулетки, проволоки, оптические свето- и радиодальномеры.
Угловые, определяющие величины горизонтальных углов. Для выполнения таких измерений применяют теодолит, буссоли, эклиметры.
Высотные, в результате, которых получают разности высот отдельных точек. Для этой цели применяют нивелиры, теодолиты-тахеометры, барометры.
Различают два метода геодезических измерений: непосредственные и посредственные (косвенные).
Непосредственные – измерения, при которых определяемые величины получают в результате непосредственного сравнения с единицей измерения.
Косвенные – измерения, при которых определяемые величины получаются как функции других непосредственно измеренных величин.
Процесс измерения включает:
Объект – свойства которого, например, размер характеризуют результат измерения.
Техническое средство – получать результат в заданных единицах.
Метод измерений – обусловлен теорией практических действий и приёмов технических средств.
Исполнитель измерений – регистрирующее устройство
Внешняя среда, в которой происходит процесс измерений.
Измерения различают равноточные и неравноточные. Равноточные – это результаты измерений однородных величин, выполняемые с помощью приборов одного класса, одним и тем же методом, одним исполнителем при одних и тех же условиях. Если хотя бы один из элементов, составляющий совокупность, меняется, то результат измерений неравноточный.
3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления
Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонение результата измерений L от истинного значения Х нумеруемой величины:
Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Недостижимое условие – истинное значение – понятие гипотетическое. Это величина, к которой можно приближаться бесконечно близко, оно не достижимо.
Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.
Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:
E = X изм – X
E = 100,05 – 100 = 0,05 (м)
Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.
Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:
C = E ср / X
C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой l допущена погрешность в 1 метр.
Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.
Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная – это сумма элементарных.
Возникают:
грубые (Q),
систематические (O),
случайные (∆).
Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений.
Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ.
Случайные погрешности измерений неизбежно сопутствуют всем измерениям. Погрешности случайные исключить нельзя, но можно ослабить их влияние на искомый результат за счет проведения дополнительных измерений. Это самые коварные погрешности, сопутствующие всем измерениям. Могут быть разные как по величине, так и по знаку.
Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей.
На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП).
Гауссом была предложена формула среднеквадратической погрешности:
∆2ср = (∆21 + ∆22 +… +∆2n) / n,
∆2 = m2 = (∆21 + ∆22 +… +∆2n) / n,
∆ср = m = √(∑∆ 2 i / n )
Формула применяется, когда погрешности вычислены по истинным значениям.
Формула Бесселя:
m = √(∑ V 2 i / (n -1))
Средняя квадратическая погрешность арифметической середины в Цn раз меньше средней квадратической погрешности отдельного измерения
М= m / Ц n
При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса.
µ 2 = P Ч m 2 – µ = m√P, m = µ / √P, т.е. средняя квадратическая погрешность любого результата измерения равна погрешности измерения с весом 1 (µ) и делённая на корень квадратный из веса этого результата (P).
При достаточно большом числе измерений можно записать ∑m2P=∑∆2P (так как ∆ = m):
µ = √(∑(∆ 2 Ч P )/ n ) , т.е. средняя квадратическая погрешность измерения с весом, равным 1 равна корню квадратному из дроби в числителе которого сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
Средняя квадратическая погрешность общей арифметической середины по формуле:
M 0 = µ / √∑ P
Подставив вместо µ её значение получим:
M0 = √(∑∆2ЧP/n) / (√∑P) = √[(∑∆2ЧP) / nЧ(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n ) / n Ч(P 1 + P 2 + … + P n ) ] – формула Гаусса , средняя квадратическая погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.
µ = √ [∑(V 2 Ч P ) / (n -1)] Это формула Бесселя для вычисления средней арифметической погрешности с измерением веса, равным 1 для ряда неравноточных измерений по их вероятнейшим погрешностям. Она справедлива для большого ряда измерений, а для ограниченного (часто на практике) содержит погрешности: mµ = µ / – это надёжность оценки µ.
Контрольная задача 1
Для исследования теодолита им был многократно измерен один и тот же угол. Результаты оказались следующими: 39˚17.4"; 39˚16.8"; 39˚16.6"; 39˚16.2"; 39˚15.5"; 39˚15.8"; 39˚16.3"; 39˚16.2". Тот же угол был измерен высокоточным угломерным прибором, что дало результат 39˚16"42". Приняв это значение за точное, вычислить среднюю квадратическую погрешность, определить надёжность СКП, найти предельную погрешность.
| № измерения | Результаты измерений, l |
Погрешности |
∆2 |
| 1 | 39˚17.4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| Сумма | 3.42 |
39˚16"42" = 39˚16.7"
Средняя квадратическая погрешность: m = √([∆ 2 ]/n) ,
m = √(3.42/8) = 0.65".
Оценка надёжности СКП: m m = m / √2n ,
mm = 0.65 / √16=0.1625≈0.16".
Предельная погрешность: ∆ пр = 3Чm ,
∆пр = 3Ч0.65" = 1.96"
Контрольная задача 2
Дана совокупность невязок треугольников триангуляции объёмом 50 единиц. Считая невязки истинными погрешностями, вычислить среднюю квадратическую погрешность и произвести надёжность СКП, вычислить предельную погрешность. На данной совокупности проверить свойство случайных погрешностей:
Lim[∆] / n =0, для чего вычислить W = [W] / n.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n , W = +2,51 / 50 = 0,05
Среднюю квадратическую погрешность в данном случае целесообразно вычислять по формуле: m = √( – [W] 2 /n ) ч (n-1) ,
m = √(76,5703 – (2,512)/50) ч 49 = 1,249
Оценку надёжности СКП по формуле: m m = m / √2(n-1) ,
mm = 1,249/ √(2Ч49) = 0,13.
Предельная погрешность по формуле: ∆ пр = 3Чm ,
∆пр = 3Ч1,249= 3,747.
Контрольная задача 5
Определить СКП расстояния вычисленного по формуле
S = √(x2 – x1)2 + (y2 – y1)2
если x2 = 6 068 740 м; y2 = 431 295 м;
x1 = 6 068 500 м; y2 = 431 248 м;
mх = my = 0,1 м.
S =√(6 068 740 - 6 068 500)2 + (431 295 - 431 248)2 =235,36
mm = 0,1/ √4 = 0,05
Контрольная задача 6
Один и тот же угол измерен 5 раз с результатами: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". Произвести математическую обработку этого ряда результатов измерений.
| Nп/п | l, ˚ | ε, " | v, " | v2, " |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| Сумма | 4 | 0 | 2,8 |
l0 – минимальное значение измеряемой величины, l0 = 60˚40" ; ε – остаток, полученный как ε = l1 - l0 ; L – наилучшее значение измеряемой величины,
L = [l]/n; m = √([ v2]/(n – 1), где v-уклонение от арифметического среднего. М – оценка точности среднего арифметического значения, М = m/√n.
L = 60˚40" + 4/5 = 60˚40,8"
m = √2,8 / 4 = 0,7"
М = 0,7"/√5 = 0,313"
Контрольная задача 7
Произвести математическую обработку результатов измерения планиметром площади одного и того же контура: 26,31; 26,28; 26,32; 26,26; 26,31 га.
| Nп/п | l, га | ε, га | v, га | v2, га |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| Сумма | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18/5 = 26,296 га
m = √0,0029/ 4 = 0,0269 га
М = 0,0269/√5 = 0,01204 га
Контрольная задача 8
При исследовании сантиметровых делений нивелирной рейки с помощью женевской линейки определялась температура в момент взятия отчета. Для пяти сантиметровых отрезков получены значения: 20,3˚; 19,9˚; 20,1˚; 20,2˚; 20,3˚. Провести математическую обработку результатов измерения.
| Nп/п | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5 | 20,3 | 0,4 | 0,14 | 0,0196 |
| Сумма | 1,3 | 0 | 0,1128 |
L = 19,9 + 1,3/5 = 20,16˚
m = √0,1128/ 4 = 0,168˚
М = 0,168/√5 = 0,075˚
3.3 Веса измерений
Вес измерения – это отвлеченное число, обратно пропорциональное квадрату СКП результата измерения.
Формула веса:
P = К / m 2 ,
где P – вес результата измерения,
К – произвольное постоянное число для данного ряда измерений,
m – СКП результата измерения.
Из формулы видно, что чем меньше СКП измерения, тем оно точнее и его вес больше.
Отношение весов двух измерений обратнопропорционально квадратам СКП этих измерений, т.е.:
P1 / P2 = m22 / m12
Если имеется ряд измерений l1, l2, …, ln, то очевидно, что вес одного измерения будет меньше веса среднего арифметического этих значений, т.е.:
где m – погрешность одного измерения,
M – погрешность среднего арифметического значения.
Тогда отношение весов обратнопропорционально отношению квадратов СКП:
PM/Pm = m2/M2;M = m/√n;
PM/Pm = m2/ (m/√n) 2 = m2/ (m2/n) = m2Чn/m2 = n.
Таким образом, вес среднего арифметического значения больше отдельно взятого значения в n раз. Следовательно, вес арифметической середины равен числу измерений, из которых она составлена.
Общая арифметическая середина из неравноточных измерений равна дроби, в числителе которой – сумма произведений средних арифметических значений из результатов измерений на их веса, а знаменатель – сумма всех весов измерений. Следовательно, вес общей арифметической середины равен сумме весов неравноточных измерений:
A0 = (a1P1 + a2P2 + … + anPn) / (P1 + P2 + … +Pn),
где A0 – общая арифметическая середина,
ai – результат отдельно взятого измерения,
Pi – вес отдельно взятого измерения.
СКП любого результата измерения равна погрешности измерения с весом 1, делимой на корень квадратный из веса этого результата, т.е.:
где m – СКП любого результата измерения;
M – погрешность измерения с весом 1;
P – вес данного результата измерения.
СКП измерения с весом 1 равна корню квадратному из дроби, в числителе которой – сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
M = √ (∑∆2P/n),
где ∆ - абсолютная погрешность неравноточного измерения;
P –его вес;
n – число измерений.
Контрольная задача 9
Результатам измерения углов соответствуют m1 = 0,5; m2 = 0,7; m3 = 1,0. Вычислить веса результатов измерений.
P = К / m 2 ;
P1 = 1 / (0,5)2 = 4;
P1 = 1 / (0,7)2 = 2,04;
P1 = 1 / (1,0)2 = 1.
Ответ: 4; 2,04; 1.
Контрольная задача 11
Найти вес невязки в сумме углов треугольника, если все углы измерены равноточно.
m = √ / (n-1), n= 3
m = √[ V21 + V22+ V23]/(3 – 1) = √[ V21 + V22+ V23]/2
P = К / √[ V21 + V22+ V23]/2 = 2 К / √[ V21 + V22+ V23] = 2/ ∑ V2i
3.4 Функции по результатам измерений и оценка их точности
В практике геодезических работ искомые величины часто получают в результате вычислений, как функцию измеренных величин. Полученные при этом величины (результаты) будут содержать погрешности, которые зависят от вида функции и от погрешности аргументов по которым их вычисляют.
При многократном измерении одной и той же величины получим ряд аналогичных соотношений:
Возведём в квадрат обе части всех равенств и сумму разделим на n:
(∆U12 + ∆U22 + … + ∆Un2) / n = k2Ч(∆l12 + ∆l22 + ... + ∆ln2) / n;
∑∆U2 / n = k2Ч(∑∆l2 / n);
m = √(∑∆U2 / n);
где ml – СКП дальномерного отсчёта.
СКП функции произведения постоянной величины на аргумент равна произведению постоянной величины на СКП аргумента.
Функция вида U = l1 + l2
Определить СКП U, где l1 и l2 – независимые слагаемые со случайными погрешностями ∆l1 и ∆l2. Тогда сумма U будет содержать погрешность:
∆U = ∆l1 + ∆l2.
Если каждую величину слагаемого измерить n раз, то можно представить:
∆U1 = ∆l1" + ∆l2" – 1-е измерение,
∆U2 = ∆l1" + ∆l2" – 2-е измерение,
…………………
∆Un = ∆l1(n) + ∆l2(n) – n-е измерение.
После возведения в квадрат обеих частей каждого равенства почленно их сложим и разделим на n:
∑∆U2 / n = (∑∆l12)/n + 2Ч(∑∆l1Ч∆l2)/n + (∑∆l22)/n.
Так как в удвоенном произведении ∆l1 и ∆l2 имеют разные знаки, они компенсируются и делим на бесконечно большое число n, то можно пренебречь удвоенным произведением.
mU2 = ml12 + ml22;
mU = √(ml12 + ml22).
СКП суммы двух измеренных величин равна корню квадратному из суммы квадратов СКП слагаемых.
Если слагаемые имеют одинаковую СКП, то:
mU = √(m2 + m2) = √2m2 = m√2.
В общем случае:
где n – количество аргументов l.
Функция вида U = l1 - l2
mU = √(ml12 + ml22).
СКП разности двух измерений величин равна корню квадратному из суммы квадратов СКП уменьшаемого и вычитаемого.
Функция вида U = l1 - l2 + l3
mU = √(ml12 + ml22 + ml32…)
СКП суммы n измеренных величин равна корню квадратному из суммы квадратов СКП всех слагаемых.
Линейная функция вида U = k1l1 + k2l2 + … + knln
mU = √[ (k1ml1)2 + (k2ml2)2 + … + (knmln)2],
т.е. СКП алгебраической суммы произведений постоянной величины на аргумент равна корню квадратному из суммы квадратов произведений постоянной величины на СКП соответствующего аргумента.
Функция общего вида U = ƒ(l1, l2, …, ln)
Это наиболее общий случай математической зависимости, включающий все рассматриваемые выше функции, являющиеся частным случаем. Это значит, что аргументы l1, l2, …, ln могут быть заданы любыми уравнениями. Для определения СКП такой сложной функции необходимо проделать следующее:
1. Найти полный дифференциал функции:
dU = (dƒ/dl1)Чdl1 + (dƒ/dl2)Чdl2 + … + (dƒ/dln)Чdln,
где (dƒ/dl1), (dƒ/dl2), …,(dƒ/dln) – частные производные функции по каждому из аргументов.
2. Заменить дифференциалы квадратами соответствующих СКП, вводя в квадрат коэффициенты при этих дифференциалах:
mU2 = (dƒ/dl1)2Чml12 + (dƒ/dl2)2Чml22 + … +(dƒ/dln)2Чmln2.
3. Вычислить значения частных производных по значениям аргументов:
(dƒ/dl1), (dƒ/dl2), …,(dƒ/dln).
И тогда mU = √[ (dƒ/dl1)2Ч ml12 + (dƒ/dl2)2Чml22 + … +(dƒ/dln)2Чmln2].
СКП функции общего вида равна корню квадратному из суммы квадратов произведений частных производных по каждому аргументу на СКП соответствующего аргумента.
3.5 Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах.
В практике геодезических работ часто одну и ту же величину измеряют дважды. Например, стороны теодолитного хода в прямом и обратном направлении, углы двумя полуприемами, превышения – по черной и красной стороне вех. Чем точнее произведены измерения, тем лучше сходимость результатов в каждой паре.
mlср. = Ѕ √∑d2/n
где d – разности в каждой паре; n – количество разностей.
Формула Бесселя:
mlср = Ѕ √∑d2/n-1
Если измерения должны удовлетворять какому-либо геометрическому условию, например, сумма внутренних углов треугольника должна быть 180˚, то точность измерений можно определить по невязкам получающимся в результате погрешностей измерений.
μ =√∑ [ f 2 / n ]/ N ,
где - СКП одного угла;
f – невязка в полигоне;
N – количество полигонов;
n – количество углов в полигоне.
4. Определение дополнительных пунктов
4.1 Цель и методы определения дополнительных пунктов
Дополнительные пункты определяются наряду со съемочной сетью в основном для сгущения существующей геодезической сети пунктами съемочного обоснования. Они строятся прямыми, обратными, комбинированными, а при наличии электронных дальномеров – линейными засечками и лучевым методом.
В некоторых случаях дополнительный пункт определяется передачей (снесением) координат с вершины знака на землю.
4.2 Передача координат с вершины знака на землю. (Решение примера)
При производстве топографо-геодезических работ в городских условиях невозможно бывает установить теодолит на пункте геодезической сети (пунктом является церковь, антенна и т.п.). Тогда и возникает задача по снесению координат пункта триангуляции на землю для обеспечения производства геодезических работ на данной территории.
Исходные данные: пункт A с координатами XA, YA; пункты геодезической сети B (XB, YB) и C (XC, YC).
Полевые измерения: линейные измерения выбранных базисов b1 и b"1; измерения горизонтальных углов Я1 , Я"1 , Я2 , Я"2 ; б, б".
Требуется найти координаты точки P – XP, YP.
Решение задачи разделяется на следующие этапы:
Решение числового примера
Исходные данные
Вычисление расстояния DАР
Решение обратных задач
Вычисление дирекционных углов αАР = αD
sin ψ = DЧsinб/ S AB; sin =174,52Ч0,66179/3068,48=0,03950;
sin ψ" = DЧsinб"/ S AС; sin `=174,52Ч0,95061/5275,51=0,03292;
ψ = arcsin 0,03950 =2 o15` 50``;
ψ"= arcsin 0,03292=1 o53` 13``;
φ = 180 o – (б+ ψ) = 180 o – (138o33` 49``+2 o15` 50``) = 39o10` 41``
φ`= 180 o – (б`+ ψ`) = 180 o – (71o55` 02``+1 o53` 13``) = 106 o11` 46``
αD = αAB ± φ =329o07` 55``+ 39o10` 41``= 8o18` 36``
αD`= αAC ± φ`=262o07` 51``+ 106 o11` 46``= 8o18` 37``
Контроль:
(αD – α"D) хmβ;
где mβ –СКП измерения горизонтальных углов.
Знак «+» или «-» в формулах вычисления дирекционного угла берется в зависимости от взаимного расположения пунктов А, Р, В и С.
(8o18` 36``-8o18` 37``) ≤ 30``
0o00` 01`` ≤ 30``
Решение прямых задач (вычисление координат т.Р)
Хp = ХА+ ∆Х,Yp = YА+ ∆Y,
Х"p = ХА+ ∆Х",Y"p = YА+ ∆Y".
∆Х= DcosαD,∆Y= DsinαD,
∆Х"= Dcosα"D,∆Y"=Dsinα"D.
Расхождение координат не должно превышать величины хmЯЧp, где p=206265", mЯ – средняя квадратическая погрешность измерения угла.
Оценка точности определения положения пункта P.
Средняя квадратическая погрешность определения отдельного пункта вычисляется по формуле:
M2p = m2X +m2Y,M2p = m2D +(DЧmα / P)2
где mD- определяется точностью линейных измерений, а m α – точностью угловых измерений.
Пример: mD =2см, mα= 5``, тогда
Mp =√ [(0,02) 2+(170Ч5/2Ч105)2] ≈ 2Ч10-2 = 0,02м.
4.3 Решение прямой и обратной засечки (по варианту задания)
Определение координат пункта прямой засечкой (формулы Юнга).
Для однократной засечки необходимо иметь два твёрдых пункта. Контроль определения осуществляется вторичной засечкой с третьего твёрдого пункта.
Исходные данные: твердые пункты А(ХАYА); B(ХBYB); С(ХСYС).
Полевые измерения: горизонтальные углы β1, β 2, β`1, β`2.
Определяется пункт P.
Формулы для решения задачи:
Хp -ХА=((ХB-ХА) ctg β 1+(YB-YА))/ (ctg β 1+ ctg β 2);
Хp= ХА+∆ХА;
Yp -YА=((YB-YА) ctg β 1+(ХB-ХА))/ (ctg β 1+ ctg β 2); Yp= YА+∆YА;
Оценка точности определения пункта P.
Вычисление СКП из 1-го и 2-го определения:
M1 =(mβЧ√(S12+ S22))/pЧsinγ1;
M2 =(mβЧ√(S12+ S22))/pЧsinγ2;
Значения величин, входящих в приведённые формулы следующие:
mβ =5``, p=206265``; γ=73˚15,9`; γ=62˚55,7`; S1=1686,77 м; S2=1639,80 м; S3=2096,62 м.
Стороны засечки найдены из решения обратных задач.
M1 = (5``Ч√2,86+2,69)/(2Ч105Ч0,958)=0,06м.
M2 = (5``Ч√2,69+4,41)/(2Ч105Ч0,890)=0,07м.
Mr = √ (M12 +M22); Mr =√ [(0,06) 2+(0,07) 2]=0,09м.
Расхождение между координатами из двух определений
r = √ [(Хp- Х`p) 2+(Yp- Y`p) 2] не должно превышать величины 3 Mr;
r =√ [(2833,82-2833,82) 2+(2116,38-2116,32) 2]=√0,0036=0,06м.
На основании неравенства r =0,06м 3Ч0,09м логично сделать вывод о качественном определении пункта P.
За окончательные значения координат принимают среднее из двух определений.
Решение числового примера
|
|
(XB- XA)ctg β1 |
|
||||
| XB- XA | YB-YA | |||||
| ctg
β1 + ctg β2
4133.41
Физико-географическая характеристика района проектирования. Характеристика главной геодезической основы. Геометрические параметры хода (на основе решения обратных геодезических задач). Критерии вытянутости хода. Расчет точности полигонометрического хода. Межевание объектов землеустройства и уведомление лиц, права которых могут быть затронуты при его проведении. Определение границ объекта землеустройства на местности, их согласование и закрепление. Государственная, опорная и межевая геодезическая сеть. Выбор методов съемки и создания геодезической основы. Планово-высотная подготовка аэроснимков и их дешифрирование. Составление плана повышения эффективности работ. Определение плановых показателей полевого подразделения. Подсчет объемов работ по объекту. Основные виды геодезических чертежей. Отличительные признаки плана и карты. Основные поверки и юстировка теодолита. Суть геодезического обоснования. Геодезическое сопровождение при монтаже колонн в стаканы фундаментов. Схема выверки колонн по вертикали. Методы топографических съемок. Теодолит Т-30 и работа с ним. Горизонтирование теодолита. Мензуальная съемка. Нивелирование поверхности. Тахеометрическая съемка. Решение инженерных задач на плане. Сравнительный анализ методов топографической съемки. В данной публикации обобщен опыт использования методов спутниковой геодезии для мониторинга геодинамических процессов, происходящих на горных предприятиях. Теория различных способов тригонометрического нивелирования. Погрешности тригонометрического нивелирования в зависимости от точности измеренных расстояний. Геодезические методы определения превышений центров пунктов государственной геодезической сети. Цель предварительных вычислений в полигонометрии. Вычисление рабочих координат. Уравнивание угловых и линейных величин. Вычисление весов уравненных значений координат узловой точки. Оценка точности полевых измерений и вычисления координат узловой точки. Электронные тахеометры: виды, принцип действия, главные преимущества, области применения и стандартные прикладные задачи. Поверки электронного тахеометра. Подготовка тахеометра к тахеометрической съемке и обработка результатов полученных измерений. Методика, позволяющая применять рекуррентный алгоритм, для контроля грубых ошибок и последующего уравнивания геодезических сетей при наблюдениях за деформациями инженерных сооружений и земной поверхности. Блок программы для анализа плановых деформаций. Рассмотрение способов образования земельных участков (раздел, выдел, объединение, перераспределение) и государственного регулирования права на их владение. Изучение основ ведения кадастрового учета. Описание процесса создания плановой геодезической сети. Освоение методики математической обработки результатов геодезических измерений в сетях сгущения. Вычисление координат дополнительных пунктов, определенных прямой и обратной многократными угловыми засечками. Уравнивание системы ходов полигонометрии. Ознакомление с геодезическими приборами. Конструктивные особенности теодолита 4Т30, нивелира 3Н-5Л и электронного тахеометра 3Та5. Геометрическое, тригонометрическое, гидростатическое, барометрическое нивелирование. Автоматизация тахеометрической съемки. Характеристика знаков закрепления геодезических сетей, их классификация по значению, местоположению, их обозначение на метности. Жилые, общественные, производственные здания. Этапы производства геодезических работ при проведении строительства объекта. Уравновешивание триангуляции, систем ходов плановой съемочной сети, теодолитных ходов с одной узловой точкой и углов сети теодолитных и полигонометрических ходов способом последовательных приближений. Схема для вычисления дирекционных углов опорных линий. |
3.2 Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления
Геодезические измерения, выполняемые даже в очень хороших условиях, сопровождаются погрешностями, т.е. отклонение результата измерений L от истинного значения Х нумеруемой величины:
Истинное – такое значение измеряемой величины, которое идеальным образом отражало бы количественные свойства объекта. Недостижимое условие – истинное значение – понятие гипотетическое. Это величина, к которой можно приближаться бесконечно близко, оно не достижимо.
Точность измерений – степень приближения его результата к истинному значению. Чем ниже погрешность, тем выше точность.
Абсолютная погрешность выражается разностью значения, полученного в результате измерения и истинного измерения величины. Например, истинное значение l = 100 м, однако, при измерении этой же линии получен результат 100,05 м, тогда абсолютная погрешность:
E = X изм – X
E = 100,05 – 100 = 0,05 (м)
Чтобы получить значение достаточно произвести одно измерение. Его называют необходимым, но чаще одним измерением не ограничиваются, а повторяют не менее двух раз. Измерения, которые делают сверх необходимого, называют избыточными (добавочными), они являются весьма важным средством контроля результата измерения.
Абсолютная погрешность не даёт представления о точности полученного результата. Например, погрешность в 0,06 м может быть получена при измерении l = 100 м или l = 1000 м. Поэтому вычисляют относительную погрешность:
C = 0,06 / 100 = 1/1667, т.е на 1667 м измеряемой l допущена погрешность в 1 метр.
Относительная погрешность – отношение абсолютной погрешности к истинному или измеренному значению. Выражают дробью. По инструкции линия местности должна быть измерена не грубее 1/1000.
Погрешности, происходящие от отдельных факторов, называются элементарными. Погрешность обобщенная – это сумма элементарных.
Возникают:
· грубые (Q),
· систематические (O),
· случайные (∆).
Грубые погрешности измерений возникают в результате грубых промахов, просчётов исполнителя, его невнимательности, незамеченных неисправностях технических средств. Грубые погрешности совершенно недопустимы и должны быть полностью исключены из результатов измерений путем проведения повторных, дополнительных измерений.
Систематические погрешности измерений – постоянная составляющая, связанная с дефектами: зрение, неисправность технических средств, температура. Систематические погрешности могут быть как одностороннего действия, так и переменного (периодические погрешности). Их стремятся по возможности учесть или исключить из результатов измерений при организации и проведении работ.
Случайные погрешности измерений неизбежно сопутствуют всем измерениям. Погрешности случайные исключить нельзя, но можно ослабить их влияние на искомый результат за счет проведения дополнительных измерений. Это самые коварные погрешности, сопутствующие всем измерениям. Могут быть разные как по величине, так и по знаку.
Если грубые и систематические погрешности могут быть изучены и исключены из результата измерений, то случайные могут быть учтены на основе глубокого измерения. Изучение на основе теории вероятностей.
На практике сложность заключается в том, что измерения проводятся какое-то ограниченное количество раз и поэтому для оценки точности измерений используют приближённую оценку среднего квадратического отклонения, которую называют среднеквадратической погрешностью (СКП).
Гауссом была предложена формула среднеквадратической погрешности:
∆ 2 ср = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n,
∆ 2 = m 2 = (∆ 2 1 + ∆ 2 2 +… +∆ 2 n) / n,
∆ ср = m = √(∑∆ 2 i / n)
Формула применяется, когда погрешности вычислены по истинным значениям.
Формула Бесселя:
m = √(∑V 2 i / (n-1))
Средняя квадратическая погрешность арифметической середины в Ön раз меньше средней квадратической погрешности отдельного измерения
При оценке в качестве единицы меры точности используют среднеквадратическую погрешность с весом равным единице. Её называют средней квадратической погрешностью единицы веса.
µ 2 = P×m 2 – µ = m√P, m = µ / √P, т.е. средняя квадратическая погрешность любого результата измерения равна погрешности измерения с весом 1 (µ) и делённая на корень квадратный из веса этого результата (P).
При достаточно большом числе измерений можно записать ∑m 2 P=∑∆ 2 P (так как ∆ = m):
µ = √(∑(∆ 2 ×P)/n), т.е. средняя квадратическая погрешность измерения с весом, равным 1 равна корню квадратному из дроби в числителе которого сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – число неравноточных измерений.
Средняя квадратическая погрешность общей арифметической середины по формуле:
M 0 = µ / √∑P
Подставив вместо µ её значение получим:
M 0 = √(∑∆ 2 ×P/n) / (√∑P) = √[(∑∆ 2 ×P) / n×(∑P)]
M 0 = √[ (∆ 1 2 P 1 + ∆ 2 2 P 2 +… + ∆ n 2 P n) / n×(P 1 + P 2 + … + P n) ] – формула Гаусса, средняя квадратическая погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.
µ = √ [∑(V 2 ×P) / (n-1)] Это формула Бесселя для вычисления средней арифметической погрешности с измерением веса, равным 1 для ряда неравноточных измерений по их вероятнейшим погрешностям. Она справедлива для большого ряда измерений, а для ограниченного (часто на практике) содержит погрешности: m µ = µ / – это надёжность оценки µ.
Контрольная задача 1
Для исследования теодолита им был многократно измерен один и тот же угол. Результаты оказались следующими: 39˚17.4"; 39˚16.8"; 39˚16.6"; 39˚16.2"; 39˚15.5"; 39˚15.8"; 39˚16.3"; 39˚16.2". Тот же угол был измерен высокоточным угломерным прибором, что дало результат 39˚16"42". Приняв это значение за точное, вычислить среднюю квадратическую погрешность, определить надёжность СКП, найти предельную погрешность.
| № измерения | Результаты измерений, l | Погрешности | ∆2 |
| 1 | 39˚17.4" | +0.7" | 0.49 |
| 2 | 16.8 | +0.1 | 0.01 |
| 3 | 16.6 | -0.1 | 0.01 |
| 4 | 16.2 | -0.5 | 0.25 |
| 5 | 15.5 | -1.2 | 1.44 |
| 6 | 15.8 | -0.9 | 0.81 |
| 7 | 16.3 | -0.4 | 0.16 |
| 8 | 16.2 | -0.5 | 0.25 |
| Сумма | 3.42 |
39˚16"42" = 39˚16.7"
Средняя квадратическая погрешность: m = √([∆ 2 ]/n),
m = √(3.42/8) = 0.65".
Оценка надёжности СКП: m m = m / √2n,
m m = 0.65 / √16=0.1625≈0.16".
Предельная погрешность: ∆ пр = 3×m,
∆ пр = 3×0.65" = 1.96"
Контрольная задача 2
Дана совокупность невязок треугольников триангуляции объёмом 50 единиц. Считая невязки истинными погрешностями, вычислить среднюю квадратическую погрешность и произвести надёжность СКП, вычислить предельную погрешность. На данной совокупности проверить свойство случайных погрешностей:
Lim[∆] / n =0, для чего вычислить W = [W] / n.
| N | W | N | W | N | W | N | W | N | W |
| 1 | +1,02 | 11 | -1,72 | 21 | -0,90 | 31 | +2,80 | 41 | -0,44 |
| 2 | +0,41 | 12 | +1,29 | 22 | +1,22 | 32 | -0,81 | 42 | -0,28 |
| 3 | +0,02 | 13 | -1,81 | 23 | -1,84 | 33 | +1,04 | 43 | -0,75 |
| 4 | -1,88 | 14 | -0,08 | 24 | -0,44 | 34 | +0,42 | 44 | -0,80 |
| 5 | -1,44 | 15 | -0,50 | 25 | +0,18 | 35 | +0,68 | 45 | -0,95 |
| 6 | -0,25 | 16 | -1,89 | 26 | -0,08 | 36 | +0,55 | 46 | -0,58 |
| 7 | +0,12 | 17 | +0,72 | 27 | -1,11 | 37 | +0,22 | 47 | +1,60 |
| 8 | +0,22 | 18 | +0,24 | 28 | +2,51 | 38 | +1,67 | 48 | +1,85 |
| 9 | -1,05 | 19 | -0,13 | 29 | -1,16 | 39 | +0,11 | 49 | +2,22 |
| 10 | +0,56 | 20 | +0,59 | 30 | +1,65 | 40 | +2,08 | 50 | -2,59 |
W = [W] / n, W = +2,51 / 50 = 0,05
Среднюю квадратическую погрешность в данном случае целесообразно вычислять по формуле: m = √( – [W] 2 /n) ÷ (n-1),
m = √(76,5703 – (2,51 2)/50) ÷ 49 = 1,249
Оценку надёжности СКП по формуле: m m = m / √2(n-1),
m m = 1,249/ √(2×49) = 0,13.
Предельная погрешность по формуле: ∆ пр = 3×m,
∆ пр = 3×1,249= 3,747.
Контрольная задача 5 Определить СКП расстояния вычисленного по формуле
S = √(x 2 – x 1) 2 + (y 2 – y 1) 2
если x 2 = 6 068 740 м; y 2 = 431 295 м;
x 1 = 6 068 500 м; y 2 = 431 248 м;
m х = m y = 0,1 м.
S =√(6 068 740 - 6 068 500) 2 + (431 295 - 431 248) 2 =235,36
m m = 0,1/ √4 = 0,05
Контрольная задача 6
Один и тот же угол измерен 5 раз с результатами: 60˚41"; 60˚40"; 60˚40"; 60˚42"; 60˚41". Произвести математическую обработку этого ряда результатов измерений.
| Nп/п | l, ˚ | ε, " | v, " | v2, " |
| 1 | 60˚41" | 1 | -0,2 | 0,04 |
| 2 | 60˚40" | 0 | +0,8 | 0,64 |
| 3 | 60˚40" | 0 | +0,8 | 0,64 |
| 4 | 60˚42" | 2 | -1,2 | 1,44 |
| 5 | 60˚41" | 1 | -0,2 | 0,04 |
| Сумма | 4 | 0 | 2,8 |
l 0 – минимальное значение измеряемой величины, l 0 = 60˚40" ; ε – остаток, полученный как ε = l 1 - l 0 ; L – наилучшее значение измеряемой величины,
L = [l]/n; m = √([ v 2 ]/(n – 1), где v-уклонение от арифметического среднего. М – оценка точности среднего арифметического значения, М = m/√n.
L = 60˚40" + 4/5 = 60˚40,8"
m = √2,8 / 4 = 0,7"
М = 0,7"/√5 = 0,313"
Контрольная задача 7
Произвести математическую обработку результатов измерения планиметром площади одного и того же контура: 26,31; 26,28; 26,32; 26,26; 26,31 га.
| Nп/п | l, га | ε, га | v, га | v2, га |
| 1 | 26,31 | 0,05 | -0,014 | 0,000196 |
| 2 | 26,28 | 0,02 | +0,016 | 0,000256 |
| 3 | 26,32 | 0,06 | -0,024 | 0,000576 |
| 4 | 26,26 | 0 | 0,036 | 0,001296 |
| 5 | 26,31 | 0,05 | -0,014 | 0,000576 |
| Сумма | 0,18 | 0 | 0,0029 |
L = 26,26 + 0,18/5 = 26,296 га
m = √0,0029/ 4 = 0,0269 га
М = 0,0269/√5 = 0,01204 га
Контрольная задача 8
При исследовании сантиметровых делений нивелирной рейки с помощью женевской линейки определялась температура в момент взятия отчета. Для пяти сантиметровых отрезков получены значения: 20,3˚; 19,9˚; 20,1˚; 20,2˚; 20,3˚. Провести математическую обработку результатов измерения.
| Nп/п | l, ˚ | ε, ˚ | v, ˚ | v2, ˚ |
| 1 | 20,3 | 0,4 | -0,14 | 0,0196 |
| 2 | 19,9 | 0 | -0,26 | 0,0676 |
| 3 | 20,1 | 0,2 | -0,06 | 0,0036 |
| 4 | 20,2 | 0,3 | 0,04 | 0,0024 |
| 5
Них не окажется нужной, то тогда средство необходимо разработать вручную, если это оправдано с точки зрения затраченного времени и материальных ресурсов. 2. Обработка геодезических измерений с использованием электронных таблиц Для первоначальной обработки информации, полученной в результате комплекса топографо-геодезических работ, мною использовалась программа “ТОГИ”, являющаяся пакетом...
На стройплощадке необходимо соблюдение требований норм и правил по технике безопасности, изложенных в главе СНиП Ш-4-80 "Техника безопасности в строительстве" и ведомственных инструкциях. К выполнению геодезических работ допускаются лица, прошедшие инструктаж, оформленный приказом по строительному управлению. Опасность получения травмы или увечья определяется в зависимости от условий рабочего...
Электронных приборов при непосредственном участии автора. Вторая глава. Во второй главе рассмотрены разработанные методы проведения исследований метрологических установок и стендов для поверки и калибровки геодезических приборов для измерения превышений. Метод исследования короткопериодической погрешности измерения вертикальных углов геодезических приборов. Важной задачей при исследовании... |
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
В ФИЗИЧЕСКОМ ПРАКТИКУМЕ
Измерения и погрешности измерений
Физика - наука экспериментальная, это означает, что физические законы устанавливаются и проверяются путем накопления и сопоставления экспериментальных данных. Цель физического практикума заключается в том, чтобы студенты изучили на опыте основные физические явления, научились правильно измерять числовые значения физических величин и сопоставлять их с теоретическими формулами.
Все измерения можно разделить на два вида – прямые икосвенные .
При прямых измерениях значение искомой величины непосредственно получается по показаниям измерительного прибора. Так, например, длина измеряется линейкой, время по часам и т. д.
Если искомая физическая величина не может быть измерена непосредственно прибором, а посредством формулы выражается через измеряемые величины, то такие измерения называются косвенными .
Измерение любой величины не дает абсолютно точного значения этой величины. Каждое измерение всегда содержит некоторую погрешность (ошибку). Ошибкой называют разность между измеренным и истинным значением.
Ошибки принято делить на систематические и случайные .
Систематической называют ошибку, которая остается постоянной на протяжении всей серии измерений. Такие погрешности обусловлены несовершенством измерительного инструмента (например, смещением нуля прибора) или методом измерений и могут быть, в принципе, исключены из конечного результата введением соответствующей поправки.
К систематическим ошибкам относятся также погрешность измерительных приборов. Точность любого прибора ограничена и характеризуется его классом точности, который, как правило, обозначен на измерительной шкале.
Случайной называется ошибка, которая изменяется в разных опытах и может быть и положительной и отрицательной. Случайные ошибки обусловлены причинами, зависящими как от измерительного устройства, (трение, зазоры, и т. п..), так и от внешних условий (вибрации, колебания напряжения в сети и т.п.).
Случайные ошибки нельзя исключить опытным путем, но их влияние на результат можно уменьшить многократными измерениями.
СРЕДНЕЕ ЗНАЧЕНИЕ И СРЕДНЯЯ АБСОЛЮТНАЯ ОШИБКА.
Предположим, что мы проводим серию измерений величины Х. Из-за наличия случайных ошибок, получаем n различных значений:
Х 1 , Х 2 , Х 3 … Х n
В качестве результата измерений обычно принимают среднее значение
Разность между средним значением и результатом i – го измерения назовем абсолютной ошибкой этого измерения
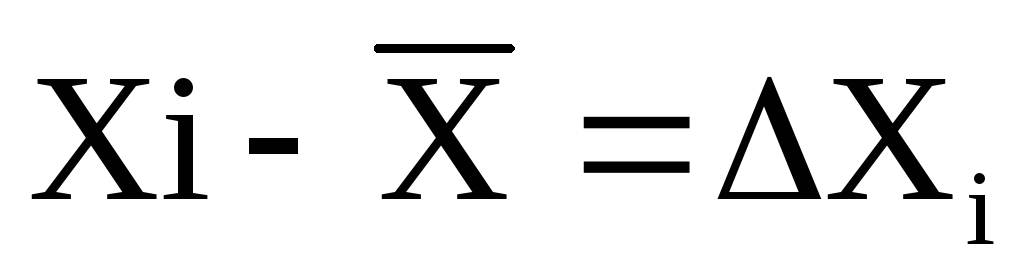
В качестве меры ошибки среднего значения можно принять среднее значение абсолютной ошибки отдельного измерения
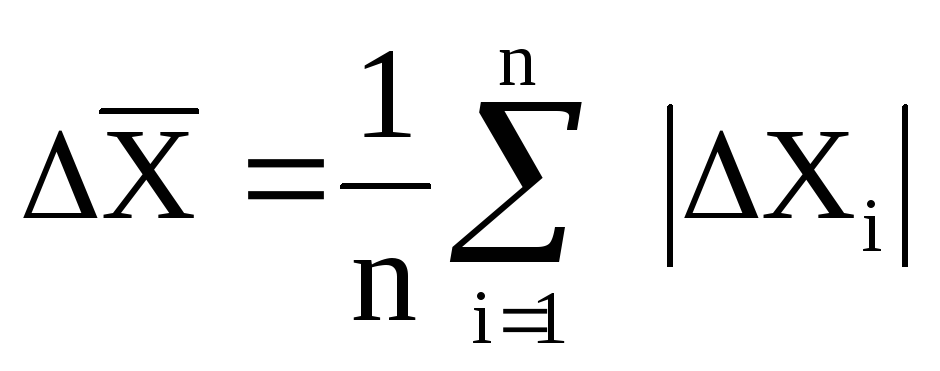(2)
Величина
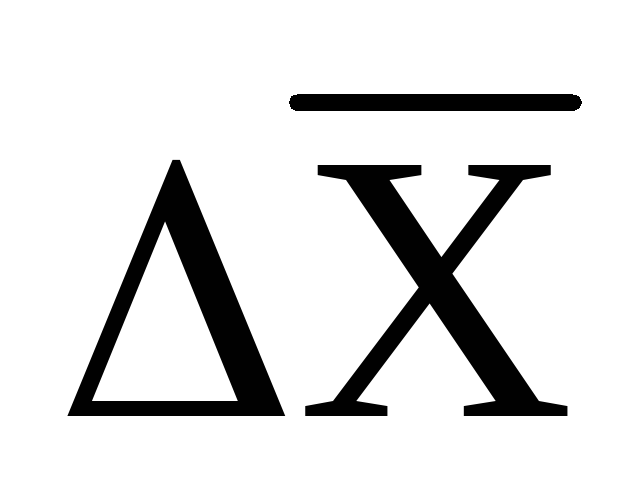называется средней арифметической (или
средней абсолютной) ошибкой.
Тогда результат измерений следует записать в виде
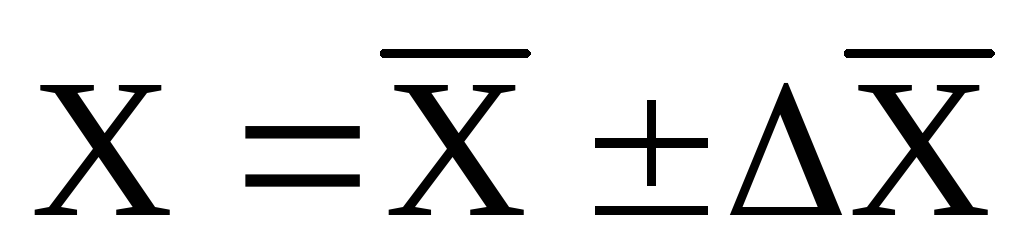(3)
Для характеристики точности измерений служит относительная ошибка, которую принято выражать в процентах
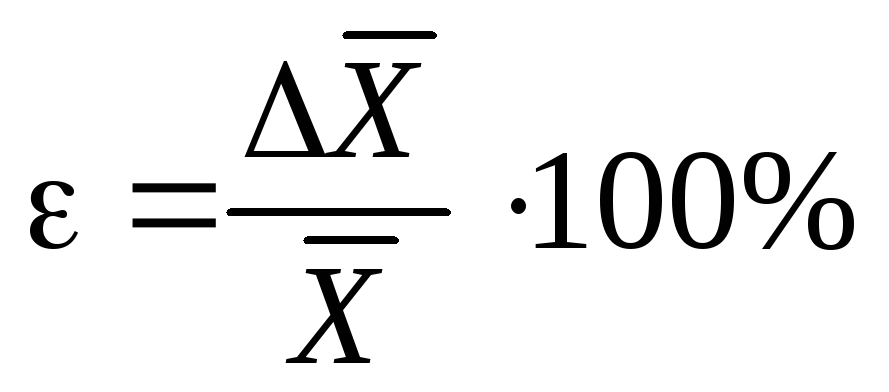(4)
СРЕДНЯЯ КВАДРАТИЧНАЯ ОШИБКА.
При ответственных измерениях, когда необходимо знать надежность полученных результатов, используется средняя квадратичная ошибка (или стандартное отклонение), которая определяется формулой
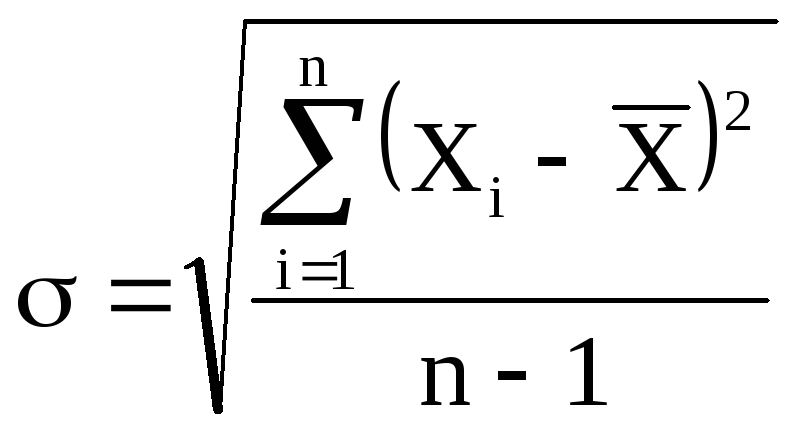(5)
Величина характеризует отклонение отдельного единичного измерения от истинного значения.
Если мы вычислили
по n
измерениям среднее значение
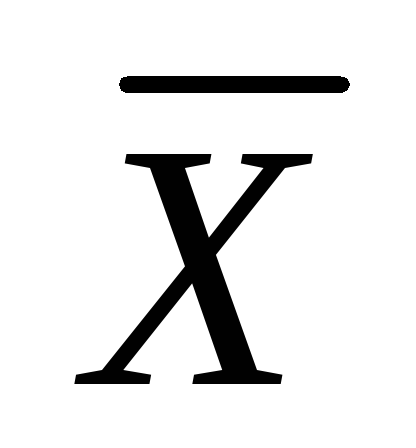по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения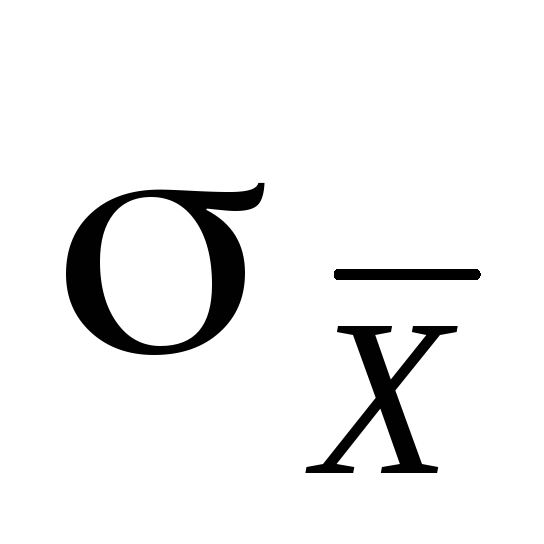
равна
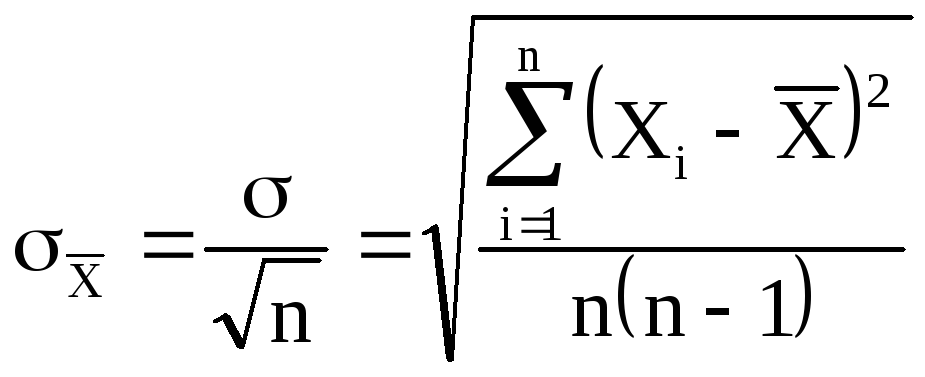(6)
где - среднеквадратичная ошибка каждого отдельного измерения, n – число измерений.
Таким образом, увеличивая число опытов, можно уменьшить случайную ошибку в величине среднего значения.
В настоящее время результаты научных и технических измерений принято представлять в виде
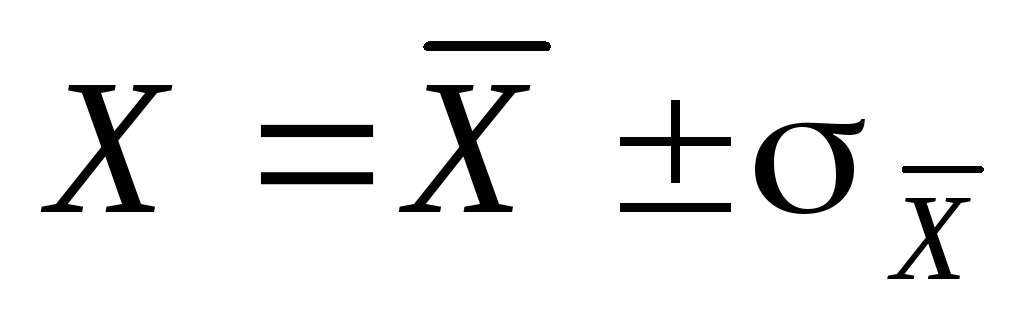(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х
с
вероятностью 68% отличается от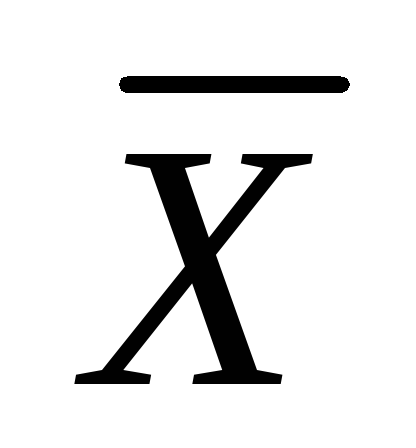не более, чем на.
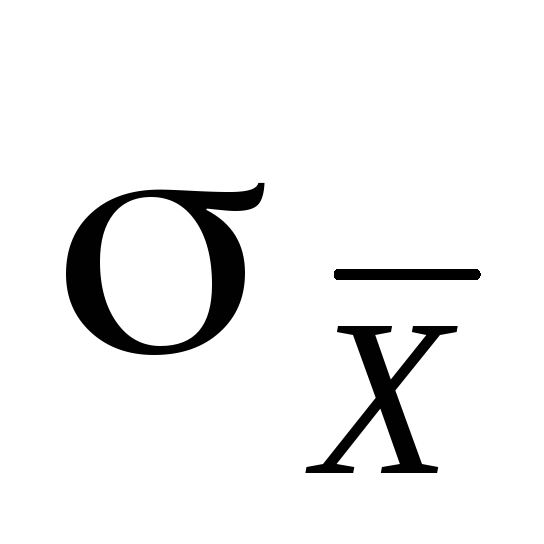При использовании же средней арифметической (абсолютной) ошибки (формула 2) о надежности результата ничего сказать нельзя. Некоторое представление о точности проведенных измерений в этом случае дает относительная ошибка (формула 4).
При выполнении лабораторных работ студенты могут использовать как среднюю абсолютную ошибку, так и среднюю квадратичную. Какую из них применять указывается непосредственно в каждой конкретной работе (или указывается преподавателем).
Обычно если число измерений не превышает 3 – 5, то можно использовать среднюю абсолютную ошибку. Если число измерений порядка 10 и более, то следует использовать более корректную оценку с помощью средней квадратичной ошибки среднего (формулы 5 и 6).
УЧЕТ СИСТЕМАТИЧЕСКИХ ОШИБОК.
Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.
Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм; для измерений штангенциркулем –
0,1 – 0,05 мм; микрометром – 0,01 мм.
Часто в качестве систематической ошибки берется половина цены деления прибора.
На шкалах электроизмерительных приборов указывается класс точности. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆Х по формуле
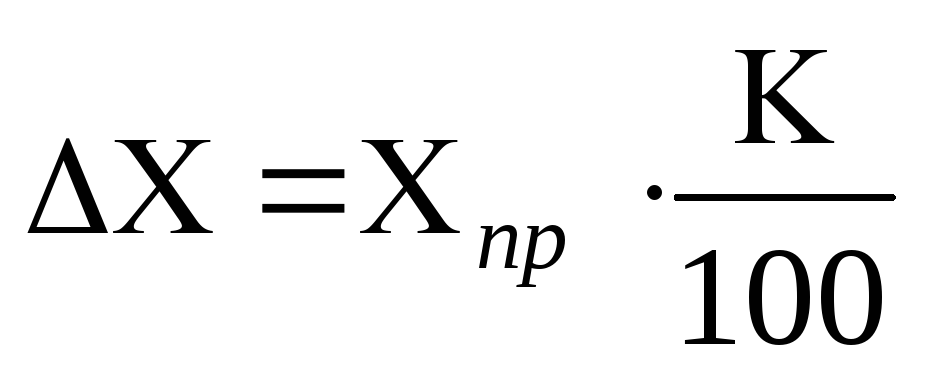
где К – класс точности прибора, Х пр – предельное значение величины, которое может быть измерено по шкале прибора.
Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более
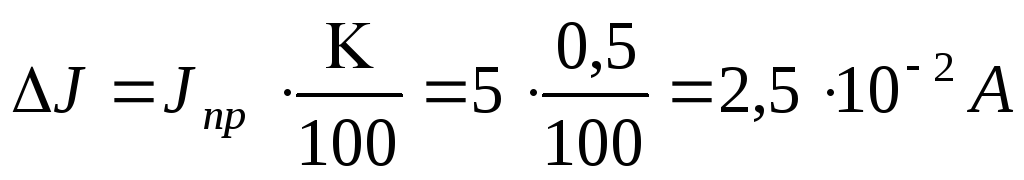
Погрешность цифрового прибора равна единице наименьшего индицируемого разряда.
Среднее значение полной погрешности складывается из случайной исистематической погрешностей.
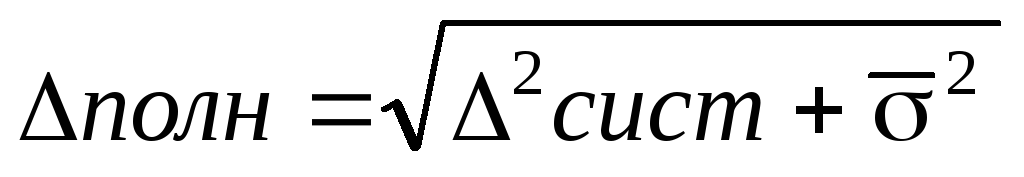
Ответ с учетом систематических и случайных ошибок записывается в виде
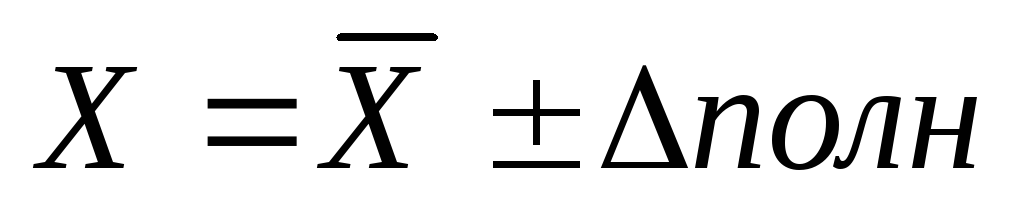
ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
В физических экспериментах чаще бывает так, что искомая физическая величина сама на опыте измерена быть не может, а является функцией других величин, измеряемых непосредственно. Например, чтобы определить объём цилиндра, надо измерить диаметр D и высоту h , а затем вычислить объем по формуле
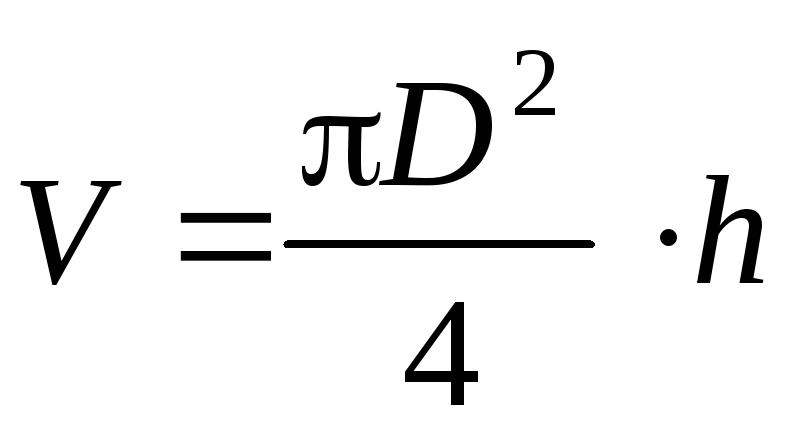
Величины D иh будут измерены с некоторой ошибкой.Следовательно, вычисленная величина V получится также с некоторой ошибкой. Надо уметь выражать погрешность вычисленной величины через погрешности измеренных величин.
Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку.
Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.
Пусть искомая величина φ является функцией нескольких переменных Х, У, Z …
φ(Х, У, Z …).
Путем прямых
измерений мы можем найти величины
,
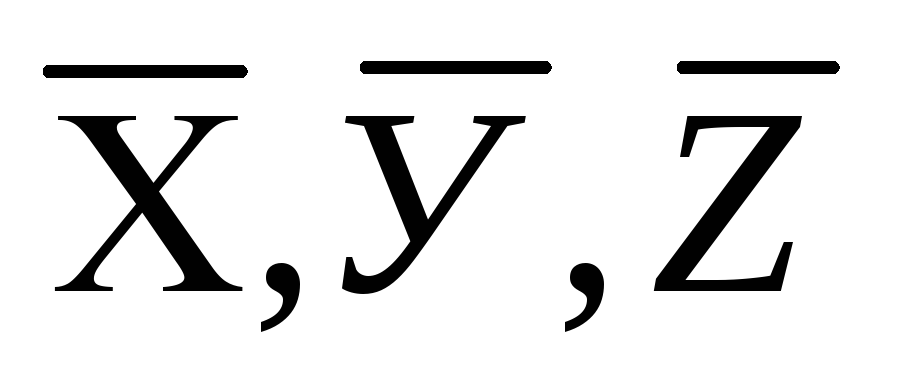а также оценить их средние абсолютные
ошибки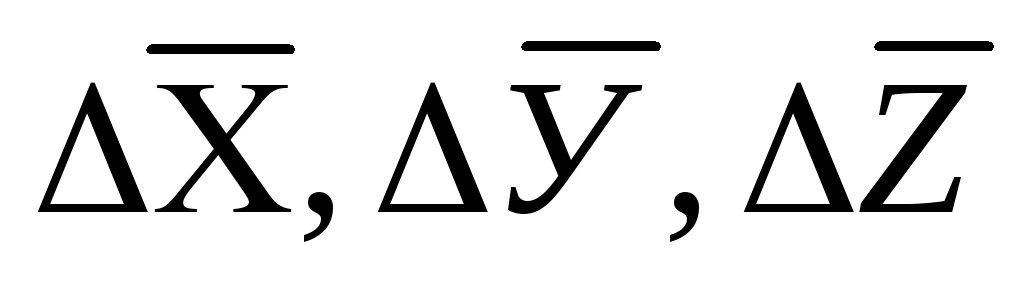
…
или средние квадратичные ошибки Х,
У,
Z …
Тогда средняя арифметическая погрешность вычисляется по формуле
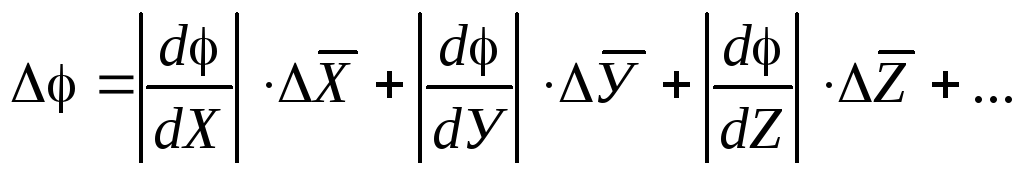
где
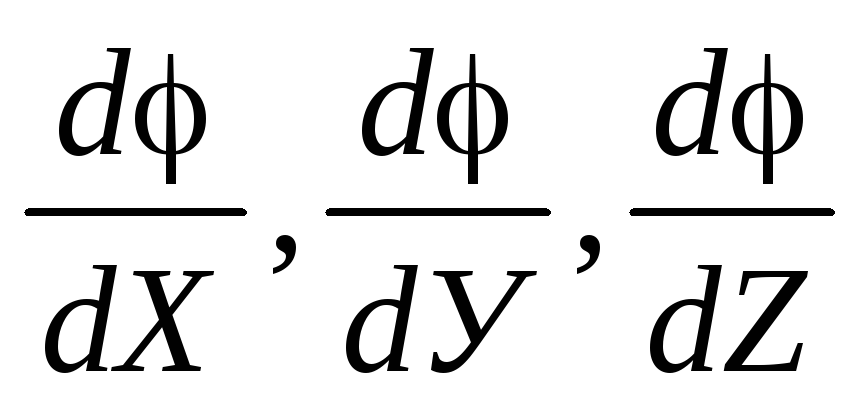- частные
производные от φ по
Х, У,
Z
.
Они
вычисляются для средних значений …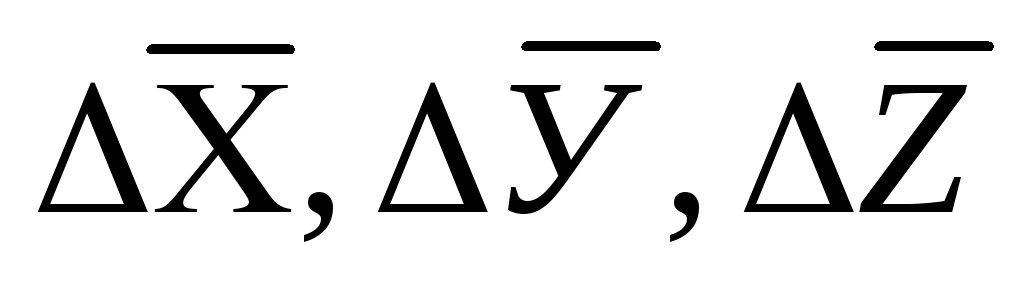
Средняя квадратичная погрешность вычисляется по формуле
Пример. Выведем формулы погрешности для вычисления объёма цилиндра.
а) Средняя арифметическая погрешность.
Величины D и h измеряются соответственно с ошибкой D и h.
б) Средняя квадратичная погрешность.
Величины D и h измеряются соответственно с ошибкой D , h .
Погрешность величины объёма будет равна
Если формула представляет выражение удобное для логарифмирования (то есть произведение, дробь, степень), то удобнее вначале вычислять относительную погрешность. Для этого (в случае средней арифметической погрешности) надо проделать следующее.
1. Прологарифмировать выражение.
2. Продифференцировать его.
3. Объединить все члены с одинаковым дифференциалом и вынести его за скобки.
4. Взять выражение перед различными дифференциалами по модулю.
5. Заменить значки дифференциалов d на значки абсолютной погрешности .
В итоге получится формула для относительной погрешности
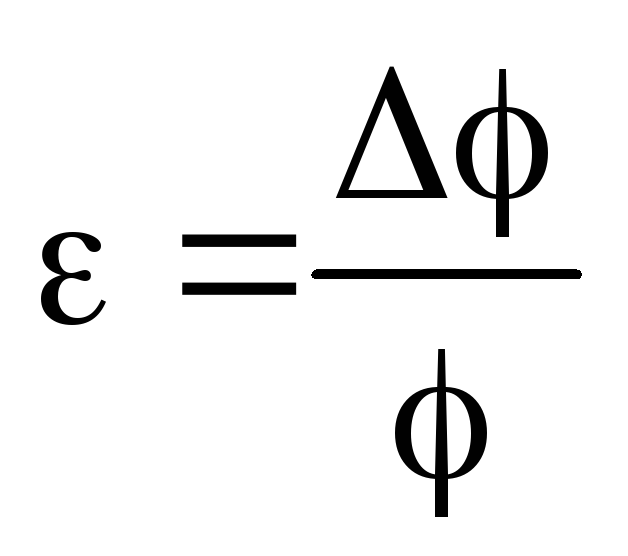
Затем, зная , можно вычислить абсолютную погрешность
=
Пример.
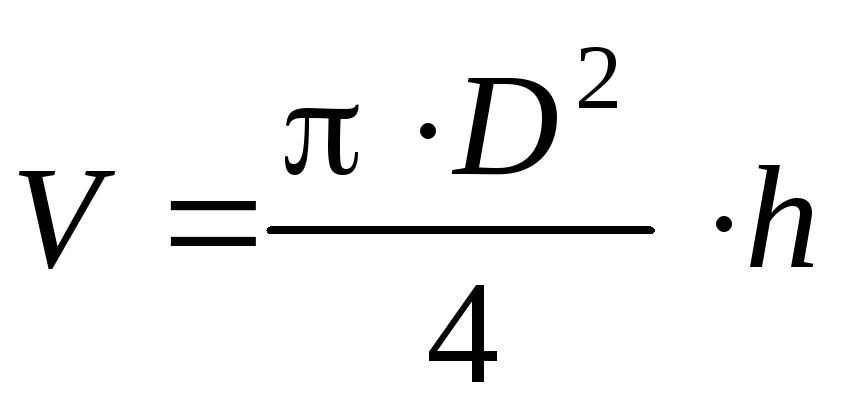
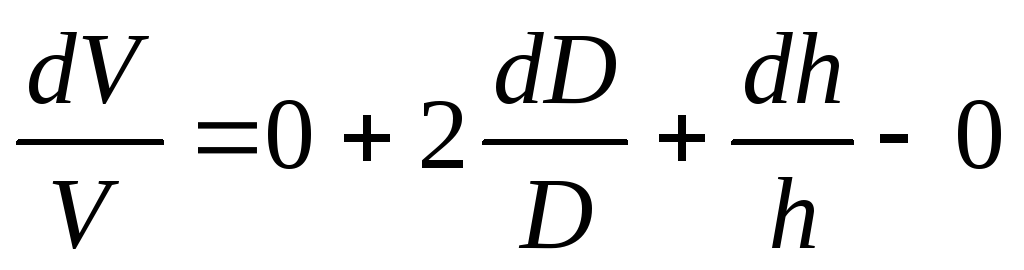
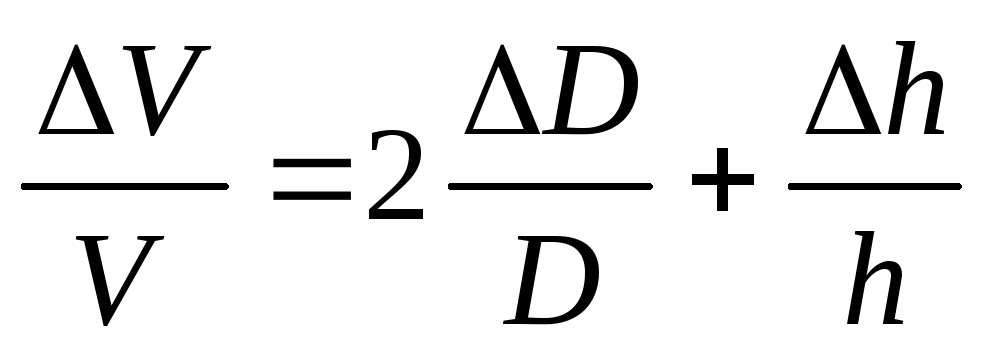
Аналогично можно записать относительную среднюю квадратичную погрешность
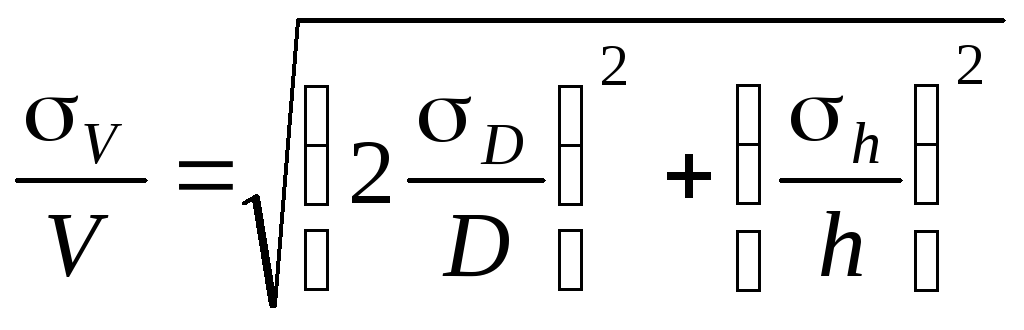
Правила представления результатов измерения следующие:
погрешность должна округляться до одной значащей цифры:
правильно = 0,04,
неправильно - = 0,0382;
последняя значащая цифра результата должна быть того же порядка величины, что и погрешность:
правильно = 9,830,03,
неправильно - = 9,8260,03;
если результат имеет очень большую или очень малую величину, необходимо использовать показательную форму записи - одну и ту же для результата и его погрешности, причем запятая десятичной дроби должна следовать за первой значащей цифрой результата:
правильно - = (5,270,03)10 -5 ,
неправильно - = 0,00005270,0000003,
= 5,2710 -5 0,0000003,
= = 0,0000527310 -7 ,
= (5273)10 -7 ,
= (0,5270,003) 10 -4 .
Если результат имеет размерность, ее необходимо указать:
правильно – g=(9,820,02) м/c 2 ,
неправильно – g=(9,820,02).
Правила построения графиков
1. Графики строятся на миллиметровой бумаге.
2. Перед построением графика необходимо четко определить, какая переменная величина является аргументом, а какая функцией. Значения аргумента откладываются на оси абсцисс (ось х ), значения функции - на оси ординат (ось у ).
3. Из экспериментальных данных определить пределы изменения аргумента и функции.
4. Указать физические величины, откладываемые на координатных осях, и обозначить единицы величин.
5. Нанести на график экспериментальные точки, обозначив их (крестиком, кружочком, жирной точкой).
6. Провести через экспериментальные точки плавную кривую (прямую) так, чтобы эти точки приблизительно в равном количестве располагались по обе стороны от кривой.
Виды погрешностей. Средняя квадратическая погрешность. - раздел Образование, Системы координат, применяемые в навигации сферическая, полярная, ортодромическая Виды Погрешностей. Практически Всегда Погрешность Включа...
Виды погрешностей. Практически всегда погрешность включает в себя две составляющие ее части: систематическую и случайную.
Δa= Δaсист + Δaслуч.
Систематической называется погрешность, которая в данных условиях сохраняет постоянное значение (или изменяется, но по известному закону).
Такие погрешности вызваны постоянно действующими причинами, в результате чего при измерении мы каждый раз «ошибаемся» на одну и ту же величину. Очень часто такие погрешности вызваны неточным изготовлением прибора (инструментальные погрешности), или постоянным внешним фактором. Например, собственное магнитное поле самолета вызывает погрешность измерения магнитного курса (девиацию), которая на каждом курсе имеет вполне определенное значение.
Систематические погрешности, поскольку они одинаковы при каждом измерении, можно один раз определить с помощью более точных приборов, а затем исключать их из результатов измерений путем ввода поправок.
Систематические погрешности не доставляют особых хлопот при навигации, поскольку после их устранения они уже отсутствуют. Поэтому далее будем считать, что систематические погрешности отсутствуют (уже учтены).
Случайная погрешность при каждом измерении принимает разное значение, причем заранее неизвестно какое именно.
А вот случайные погрешности в принципе устранить нельзя, поскольку они при каждом измерении различны. И они всегда остаются неизвестными.
Определить численные значения случайных погрешностей невозможно, однако пилот постоянно должен иметь в виду, что эти погрешности существуют и иметь представление об их возможных значениях. Наличие неопределенности в результатах измерений является одним из основных факторов, усложняющих навигацию и делающих ее не только наукой, и искусством.
Случайным событием называют событие, которое при данных условиях может произойти или не произойти. Степень возможности наступления такого события численно характеризуют величиной вероятности. Вероятность Р – это число, которое может лежать в пределах от 0 до 1. Если при данных условиях событие никогда не происходит, его называют невозможным событием и его вероятность равна нулю. Если же оно при данных условиях происходит всегда, то его называют достоверным и приписывают ему вероятность равную единице. Если, например, Р=0,3, то это означает, что в среднем в 30 случаях из 100 событие произойдет. Именно в среднем, поскольку событие является случайным. Если создать необходимые для наступления события условия и провести серию из 100 опытов, то событие может произойти, например, 23 раза, или 32 раза… Если провести несколько серий таких опытов, или одну серию из тысячи, десяти тысяч, миллиона опытов, то, чем большее количество опытов проведено, тем ближе среднее количество наступлений события будет ближе к 30% от общего количества опытов (если Р=0,3).
Каким же образом можно описать случайные погрешности, если они не имеют какого-либо определенного значения? Часто их характеризуют величиной средней квадратической погрешности (СКП), которая обозначается буквой σ (сигма). Так, например, СКП измерения величины a будем обозначать σa.
СКП является характеристикой степени рассеяния измеренного значения величины вокруг фактического ее значения. Чем больше σa, тем больше рассеяны (разбросаны) измеренные в разных опытах значения вокруг фактического значения величины.
На рис. 2.19 геометрически представлены в виде числовой оси возможные значения измеряемой величины a и отмечено фактическое ее значение. Крестиками на шкале обозначены полученные в результате нескольких опытов измеренные значения. В первом случае разброс измеренных значений вокруг фактического больше, чем во втором случае, следовательно «сигма», которая и характеризует степень разброса, во втором случае меньше.
Рис. 2.19. Средняя квадратическая погрешность
По величине СКП можно судить о вероятностях того, что измеренное значение примет то или иное значение. Но для этого недостаточно знать СКП, нужно также знать, какому закону распределения подчиняется данная случайная погрешность. Многие случайные величины подчиняются нормальному (гауссовскому) закону распределения. Для этого закона полезно запомнить следующие значения.
Если систематическая погрешность отсутствует и в результате измерения получено значение aизм, то фактическое значение величины лежит в пределах (рис. 2.20):
aизм ± σa с вероятностью Р=0,68;
aизм ± 2σa с вероятностью Р=0,95;
aизм ± 3σa с вероятностью Р=0,997.
Рис. 2.20. Некоторые вероятности для нормального закона распределения
Например, с помощью компаса измерен курс γ=100º, а точность компаса характеризуется СКП σγ =2º . Это означает, что фактический курс (который так и останется нам неизвестным) в среднем :
в 68 случаях из 100 лежит в пределах 100º ±2º, то есть в интервале 98º…102 º;
в 95 случаях из 100 лежит в пределах 100º ±4º, то есть в интервале 96º…104º;
в 997 случаях из 1000 лежит в пределах 100º ±6º, то есть в интервале 94º …106º.
Значение вероятности Р =0,997 настолько близко к единице, что соответствующее ей значение погрешности в «три сигмы» часто называют максимальной погрешностью. На самом деле погрешность может его и превысить. Правда, редко – в среднем в трех случаях из тысячи.
В технических описаниях приборов и оборудования их точность может быть указана непосредственно в виде СКП и тогда все понятно. Но иногда ее указывают, например, так: «погрешность измерения пеленга ±1,5º». Разумеется, это не означает, что такой пеленгатор «ошибается» каждый раз на 1,5º . Это также не означает, что он не может ошибиться более , чем на 1,5º. Как правило, указанное таким образом значение погрешности соответствует вероятности Р =0,95. То есть в среднем в 95 случаях из 100 погрешность не превысит (в большую или меньшую сторону) значения в 1,5º.
Соответственно, в пяти случаях из ста погрешность может быть и больше. Для нормального закона распределения погрешности вероятность 0,95 соответствует удвоенной СКП. Следовательно, СКП измерения пеленга в данном примере составит 0,75º.
Конец работы -
Эта тема принадлежит разделу:
Рис Полярная система координат... Дальность расстояние от начала системы координат до объекта точки...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Системы координат, применяемые в навигации (сферическая, полярная, ортодромическая).
Если очень высокая точность решения навигационных задач не требуется, то Землю можно рассматривать как сферу. В этом случае используется нормальная сферическая система координат, полюсы кото
Навигационные и пилотажные элементы.
Пилотажные элементы. Навигация и пилотирование являются процессами управления движением ВС. Чтобы описывать это движение, используются величины, называемые навигационными и пилотаж
Ветер и его характеристики. Эквивалентный ветер.
Воздушные массы атмосферы практически всегда находятся в движении, которое вызвано различием температуры и давления в различных районах земной поверхности. Причины и характер такого движения изучае
Навигационный треугольник скоростей. Зависимость путевой скорости и угла сноса от угла ветра.
ВС движется относительно воздушной массы с истинной воздушной скоростью V, воздушная масса относительно земли со скоростью U,и скорость перемещения ВС относительно
Принципы измерения курса и виды курсовых приборов.
Курс характеризует направление продольной оси ВС в горизонтальной плоскости, то есть показывает, куда направлен «нос» самолета. Он имеет большое значение для навигации, поскольку одновременно являе
Девиация, её виды, учёт в полёте.
Очевидно, что в одной и той же точке пространства не могут одновременно существовать два магнитных поля, два вектора напряженности – Земли (H) и самолета (F). Эти
Практические рекомендации по применению магнитных компасов.
1. Следует помнить, что в полярных районах, где велико магнитное наклонение и, следовательно, мала горизонтальная составляющая магнитного поля Земли, магнитные компасы работают неустойчиво и могут
Гироскопический принцип измерения курса. Выставка оси гироскопа, горизонтальная и азимутальная коррекция.
Гироскоп (от древнегреческих «вращать» и «смотреть») – это в принципе любое вращающееся тело. В современной технике гироскоп представляет собой достаточно массивный ротор с большой скоростью
Гирополукомпас ГПК-52. Ортодромичность гирополукомпаса.
Гирополукомпас ГПК-52. Принцип работы гироскопических курсовых приборов рассмотрим на примере одного из простейших устройств такого рода− гирополукомпаса ГПК-52.
Ортодромичность курсового гироскопа
Теперь после анализа поведения курсового гироскопа на неподвижном самолете рассмотрим, как он будет вести себя в случае, когда ВС перемещается по ортодромической линии пути. Общий случай – п
Опорный меридиан и ортодромический курс. Преобразование курсов.
Ось гироскопа в начале полета может быть выставлена по абсолютно любому направлению. Пилоты привыкли, что курс 0° – это на север, 90° – на восток и т.д. Поэтому, чтобы численные значения гир
Основные сведения о курсовых системах. Режим магнитной коррекции.
Каждый из двух рассмотренных принципов измерения курса – магнитный и гироскопический – имеет свои достоинства и недостатки.
Магнитный компас обладает тем достоинством, что позволяет именно
Режим магнитной коррекции
Как уже отмечалось, в режиме «ГПК» курсовая система работает аналогично обычному гирополукомпасу, поэтому этот режим не требует дополнительного отдельного рассмотрения.
Рассмотрим работу к
Понятие о радиовысотомерах
Радиовысотомер (РВ) является автономным радиотехническим устройством. Это означает, что для его работы используются радиоволны и не требуется какого-либо оборудования на земле.
Разл
Принцип работы, устройство и погрешности барометрического высотомера.
По принципу своего устройства барометрический высотомер по сути представляет собой барометр-анероид с тем лишь отличием, что его шкала отградуирована не в единицах давления, а в единицах выс
Погрешности барометрического высотомера
Барометрический высотомер имеет ряд погрешностей, различающихся по вызывающим их причинам. Погрешности, вызванные разными факторами, складываются, образуя одну общую погрешность – разность между пр
Уровни начала отсчета барометрической высоты
В принципе, путем установки давления на шкале барометрического высотомера пилот может сам выбрать уровень, от которого он желает отсчитывать высоту. Но с точки зрения безопасности полетов необходим
Правила установки давления на шкале барометрического высотомера
Рассмотрим порядок установки давления при полете по ППП.
Традиционная технология, принятая в нашей стране, предусматривает, что перед вылетом все члены экипажа на своих высотомерах
Однострелочные указатели скорости
В уравнение Бернулли входят плотности воздуха ρ в обоих сечения струйки. Для небольших скоростей (до 400-450 км/ч) и высот полета (до 4000-5000 м) воздух можно считать несжимаемым
Комбинированные указатели скорости
На больших скоростях и высотах разность истинной и приборной скоростей становится уже значительной. Кроме того, на больших скоростях и высотах начинает заметно сказываться сжимаемость воздуха. Поэт
Погрешности указателей скорости
Инструментальные погрешности ΔVи возникают из-за несовершенства конструкции прибора и неточности его регулировки. Каждый экземпляр прибора имеет свои значения инструментальны
Понятие о счислении
При выполнении любого полета члены летного экипажа должны в любой момент времени знать текущее местонахождение ВС. Определение места самолета – одна из основных задач аэронавигации. В аэронавигации
Графическое счисление пути
Полная прокладка. Целью полной прокладки является определение текущего МС и поэтому она, конечно, выполняется во время полета. Не следует думать, что в каждом полете пилот или штурман выполн
Принцип автоматизированного счисления частноортодромических координат.
Счисление – это расчет текущих координат, поэтому основной частью любой автоматизированной системы счисления пути является навигационный вычислитель. Он может быть аналоговым, то есть основа
ДИСС. Курсодоплеровское и курсовоздушное счисление.
Доплеровский измеритель скорости и сноса (ДИСС) – бортовое радиотехническое устройство, позволяющее измерять на борту ВС его путевую скорость и угол сноса.
ДИСС основан на использов
Основные правила аэронавигации. Контроль пути и его виды.
На протяжении всего полета экипаж обязан выполнять следующие основные правила аэронавигации.
1) Контроль выдерживания заданной траектории полета с периодичностью, необходимой для обеспечен
Визуальная ориентировка.
Визуальная ориентировка – способ определения МС, основанный на сличении карты с пролетаемой местностью.
Для визуальной ориентировки используются ориентиры.
Навигационный ориентир
Обобщённый метод линий положения. Навигационный параметр, поверхность и линия положения.
Навигационный параметр. Место самолета можно определить с помощью различных технических, в том числе радионавигационных средств и разными методами. Но как показал профессор В.В
Поверхность и линия положения.
Если в какой-то точке пространства навигационный параметр имеет какое-то определенное значение, то это не вовсе не значит, что в других точках его значения должны быть обязательно другие. Наверняка
Виды линий положения.
В навигации чаще всего используются навигационные параметры, которые являются геометрическими величинами, то есть расстояниями, углами и пр. В этом случае каждому виду навигационного параметра соот
Навигационная характеристика радиокомпасной системы.
Радиокомпасная система включает в себя наземную радиостанцию и бортовой пеленгатор, называемый автоматическим радиокомпасом (АРК). В качестве радиостанций могут использоваться специально установлен
Принцип работы АРК и порядок его настройки.
Принцип работы радиокомпаса основан на направленном приеме радиоволн. АРК включает в себя следующие основные составные части:
– поворотную рамочную антенну;
– ненаправленную (шлей
Способы полёта на РНТ (пассивный, курсовой, активный).
Способы полета на или от радиостанции. Как показано ранее, КУР не является навигационным параметром, поскольку в одной и той же точке пространства может иметь любое значение в
Контроль пути по направлению с помощью АРК при полёте на и от РНТ.
Условие контроля пути по направлению.
Существует общий термин «радионавигационная точка» (РНТ), которым можно обозначать любое наземное радионавигационное средство: ОП
Контроль пути по дальности с помощью АРК.
Контроль пути по дальности – это определение пройденного или оставшегося расстояния до ППМ. Для его выполнения также можно использовать АРК и ОПРС. Но для этого ОПРС, конечно, должна находиться не
Расчёт ИПС и определение МС по двум радиостанциям.
Для решения некоторых навигационных задач, например, для определения МС, необходимо проложить на карте ЛРПС. Для этого необходимо сначала определить пеленг самолета. Поскольку на любой карте нанесе
Определение места самолета по двум радиостанциям
Определение места самолета – это полный контроль пути, поскольку если известно место самолета, то можно определить и уклонение от ЛЗП (контроль пути по направлению), и пройденное или оставшееся рас
Исправление пути с выходом в ППМ и с углом выхода.
Исправление пути с выходом в ППМ. Исправление пути это действия по выводу ВС на заданную траекторию после того, как отклонение от нее обнаружено.
Один из способов испр
Исправление пути с углом выхода
Ранее в главе 1 уже был рассмотрен один из способов исправления пути – с выходом в ППМ. Но такой способ в гражданской авиации применим главным образом при небольших линейных уклонениях, например, н
Указатели типа РМИ и УГР. Полёт по ЛЗП с их использованием.
Наиболее распространены так называемые радиомагнитные индикаторы (РМИ). По-английски они называются точно так же – Radio Magnetic Indicator (RMI). В некоторых типах отечественных навигационных комп
Полет в створе радиостанций
Если полет должен выполняться по ЛЗП, на которой установлены две радиостанции, то говорят о полете в створе радиостанций. Если ВС летит между РНТ (одна впереди, а другая сзади), то створ называется
Минимальная и максимальность действия РНС.
Минимальная дальность действия. В вертикальной плоскость диаграмма направленности большинства наземных радионавигационных средств (радиостанций, радиомаяков) выглядит примерно
Навигационная характеристика радиопеленгаторной системы.
Характеристика радиопеленгаторной системы. Радиопеленгаторная система является в первую очередь средством управления воздушным движением (УВД). С ее помощью диспетчер УВД на зе
Радиомаячная система VOR и её применение для полёта по ЛЗП, определение МС.
Принцип действия VOR. Радиомаячная угломерная система VOR (Very High Frequency Omni-directional Range) включает в себя наземное оборудование – радиомаяк VOR, и бортовое оборудо
Определение места самолета по одной радиостанции
В соответствии с обобщенным методом линий положения для определения МС необходимо два навигационных параметра и две соответствующие им линии положения. Казалось бы, что если радиостанция только одн
Принцип действия дальномерных систем. Наклонная и горизонтальная дальности.
Характеристика DME. Дальномерная радионавигационная система (ДРНС) включает в себя наземное оборудование (дальномерный радиомаяк) и бортовое оборудование (самолетный дальномер)
Угломерно-дальномерные системы. Навигационная характеристика РСБН.
Угломерно-дальномерными радионавигационными системами (УДРНС) называют такие системы, которые позволяют одновременно измерить два навигационных параметра – пеленг и дальность. С помощью УДРНС можно
Навигационная характеристика наземных РЛС и их применение для контроля и исправления пути.
Понятие о радиолокации. Под радиолокацией (от «радио» и location (лат.) – определять местоположение) в широком смысле слова понимают способы определения местоположения и характ
Понятие о зональной навигации.
Навигационное наведение. Невозможно понять, что такое зональная навигация, да и современная навигация вообще, если не иметь представления о таком понятии, как навигационное нав
Принцип работы бортовой РЛС. Органы управления БРЛС «Гроза».
Бортовая радиолокационная станция (БРЛС) является автономным радиотехническим средством, позволяющим наблюдать радиолокационное изображение пролетаемой местности и окружающей воздушной обстановки,
Способы определения МС с помощью БРЛС (угломерный, дальномерный, угломерно-дальномерный).
С помощью БРЛС можно определить МС гораздо точнее, чем обзорно-сравнительным способом. Для этого на экране локатора нужно измерить курсовой угол и дальность до ориентира.
Курсовой угол ори
Обзорно-сравнительный способ ориентировки по БРЛС и определение с её помощью путевой скорости и угла сноса.
Благодаря тому, что на экране БРЛС формируется изображение пролетаемой местности, пилот может вести ориентировку путем сопоставления радиолокационного изображения с полетной картой, наподобие того,
Определение путевой скорости и угла сноса по БРЛС
Определение путевой скорости. Все ориентиры на экране по мере движения ВС перемещаются в сторону, противоположную направлению движения ВС, то есть, на экране примерно вниз. Име
Принцип инерциального счисления пути
Инерциальные навигационные системы (ИНС) основаны на измерении ускорений ВС по осям системы координат. Ускорения измеряются устройствами, называемыми акселерометрами. Принцип действия
Параметры, определяемые с помощь ИНС. Бесплатформенные ИНС.
Параметры, определяемые с помощью ИНС.Инерциальные системы предназначены для определения координат места самолета. Но в процессе их определения можно получить значения многих д
Бесплатформенные инерциальные навигационные системы
На протяжении многих десятилетий усилия инженеров, разрабатывавших традиционные ИНС, были направлены на уменьшение собственного ухода гироскопов, удерживающих гироплатформу в заданном положении. Не
Расчёт курса, скорости и времени по известному ветру.
Рассмотрим порядок решения задачи на примере со следующими исходными данными:
V = 400;
ЗМПУ =232;
δ =290;
U = 70;
S = 164;
ΔМ= –4.
Определение ветра в полёте.
Дано:
V=680;
W=590;
МК=312;
УС=+8;
ΔМ= –4.
Найти: δн, δ, U.
Расчёт истинной скорости по широкой стрелке.
Истинная скорость по показанию широкой стрелки КУС рассчитывается по формуле:
Vи = Vпр + ΔVи + ΔVa + ΔVсж + ΔV
